匀减速直线运动问题
要点 (Cues)
- 匀减速运动
- v-t图为直线
- 平均速度
- 相似比例
- 线性关系
- 时间中点的速度
详情 (Notes)
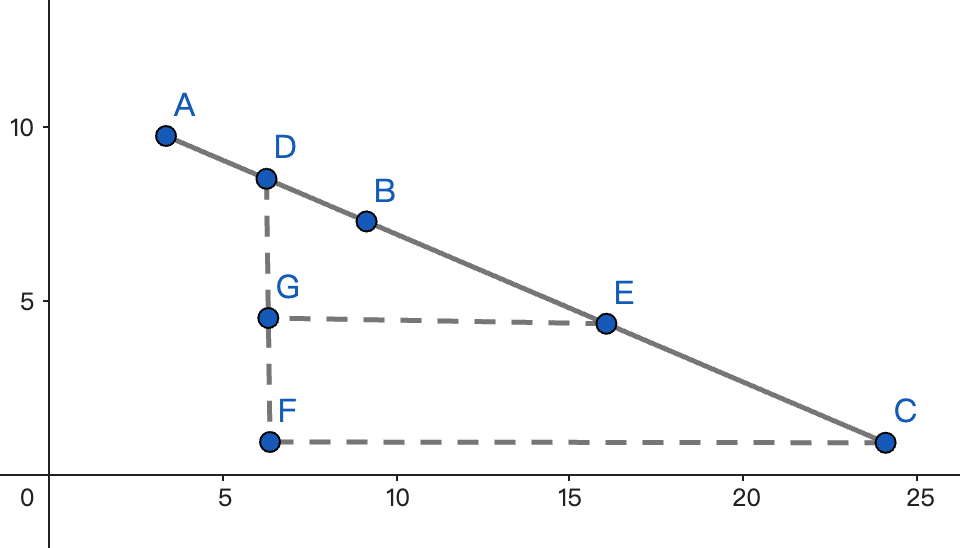
一辆公交车以匀减速直线行驶经过A,B,C三点,已知BC的距离时AB的2倍,AB段的平均速度时10m/s,BC的平均速度是5m/s,求经过C点的速度
- 基本概念
- 匀减速运动:加速度恒定为负
- v-t图是斜率恒定的直线
- ,平均速度出现在时间中点,也就是平均速度等于时间中点时的瞬时速度
- 解题思路一:基于速度变化比
- 列出平均速度方程:
- (v₀+v₁)/2 = 10
- (v₁+v₂)/2 = 5
- BC时间是AB的4倍(距离2倍,速度1/2)
- 速度变化比:(v₀-v₁)/(v₁-v₂) = 1/4
- 解方程得v₂ = 1m/s
- 解题思路二:基于斜率相等
- 找到平均速度对应的时间中点
- AB中点到BC中点:2.5t
- BC中点到C点:2t
- 斜率相等:(10-5)/2.5t = (5-x)/2t
- 解得x = 1m/s
总结 (Summary)
- 解题关键点:
- 利用匀减速运动v-t图为直线
- 时间比
- 平均速度出现在时间中点,平均速度也是时间中点的瞬时速度
- 速度变化与时间成正比
- 两种解法比较:
- 第一种更系统但计算复杂
- 第二种更巧妙且计算简单
- 都体现了物理量之间的线性关系
- 启示:
- 注意时间、速度、距离三者关系
- 善用图象特性简化计算
- 寻找物理量间的比例关系
- 知识点