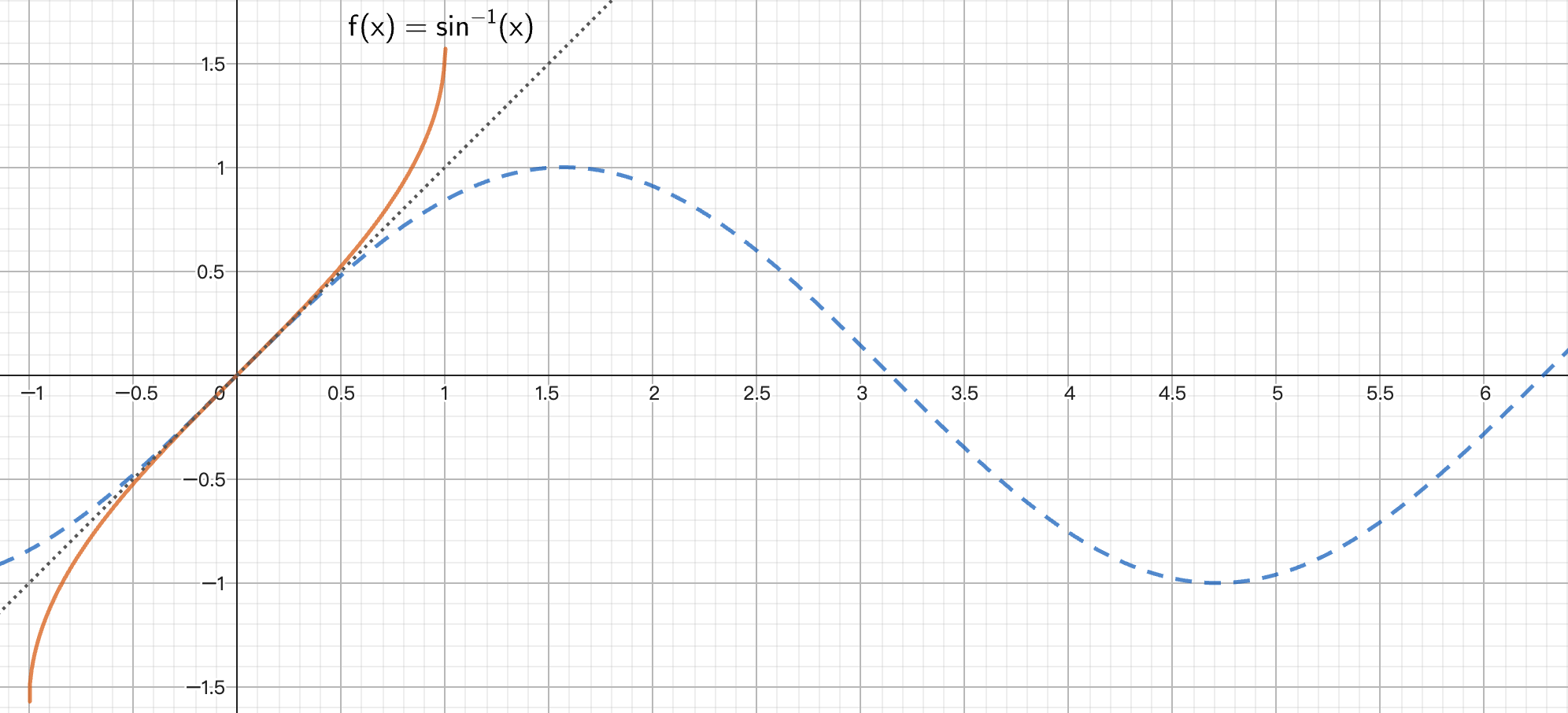
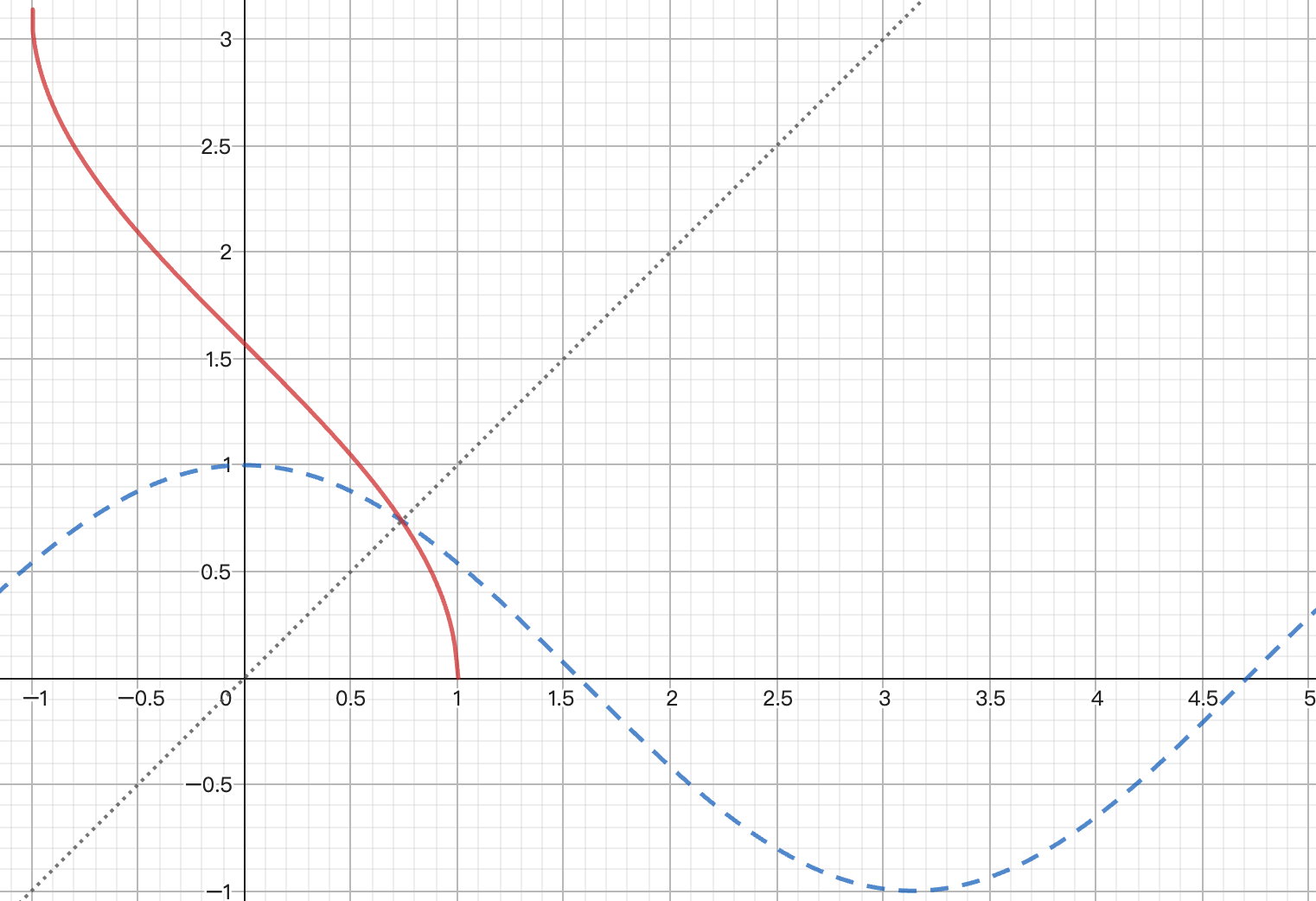
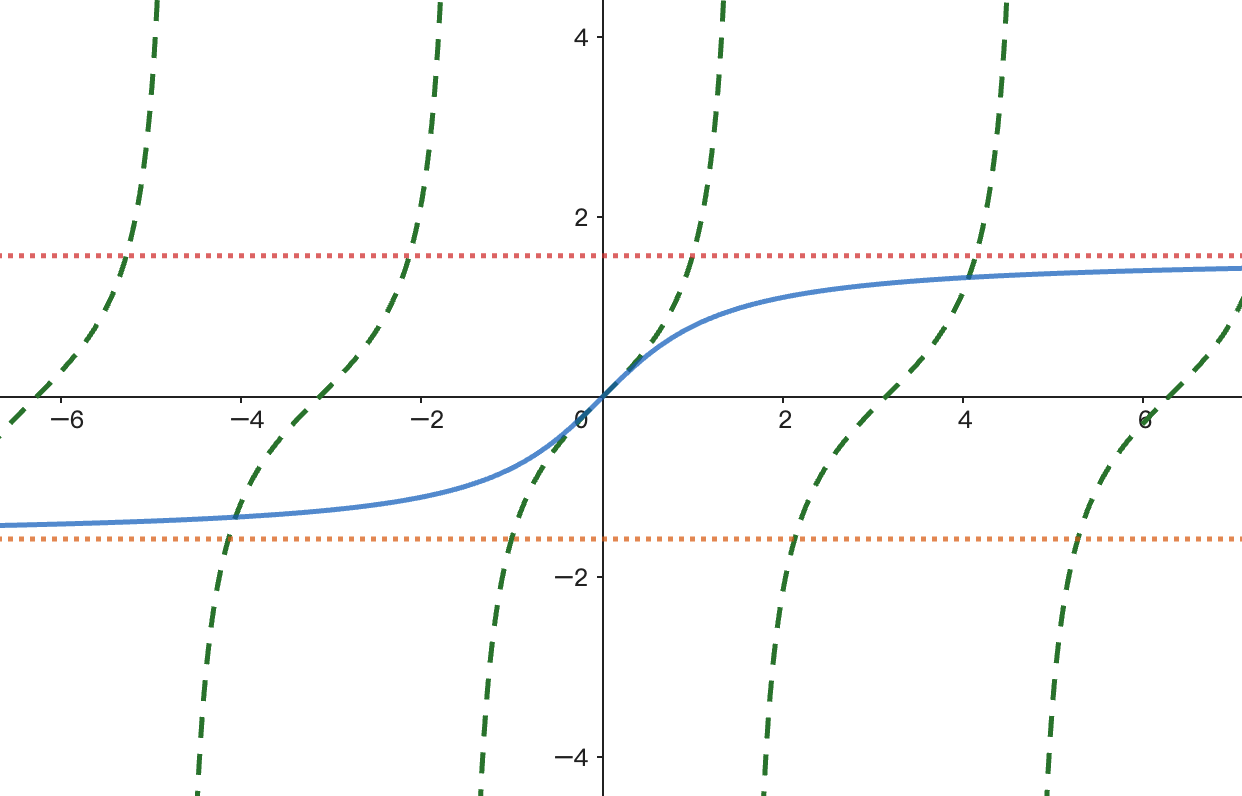
反三角函数的图像是通过将原三角函数在特定区间内的图像关于 y=x 线对称翻转得到，这种翻转使得原函数的定义域变为反函数的值域，原函数的值域变为反函数的定义域。

基本特征

函数	定义域	值域	单调性	对称性
${\sin }^{-1}x$	[-1, 1]	$[-\frac{\pi }{2},\frac{\pi }{2}]$	递增	奇函数
${\cos }^{-1}x$	[-1, 1]	$[0,\pi ]$	递减	非奇非偶
${\tan }^{-1}x$	$\mathbb{R}$	$(-\frac{\pi }{2},\frac{\pi }{2})$	递增	奇函数

反正弦函数

• 过原点
• 单调递增
• 原点对称
• 无渐近线
• 端点垂直切线

反余弦函数

• 过点(1,0)
• 单调递减
• 无对称性
• 无渐近线
• 端点垂直切线

反正切函数

• 过原点
• 单调递增
• 原点对称
• 水平渐近线 $y=\pm \frac{\pi }{2}$
• 处处有限斜率

常见误区

1. 反三角函数不是周期函数
2. 定义域和值域的限制是必要的
3. 不是所有反三角函数都有对称性
4. 导数与原三角函数不同
5. 图像翻转需考虑定义域限制