指数函数图像的基本特征
基本特征:
- 必过点(0,1)
- 图像永远在x轴上方
- x轴是其水平渐近线
- 定义域:全体实数
- 值域:所有正实数
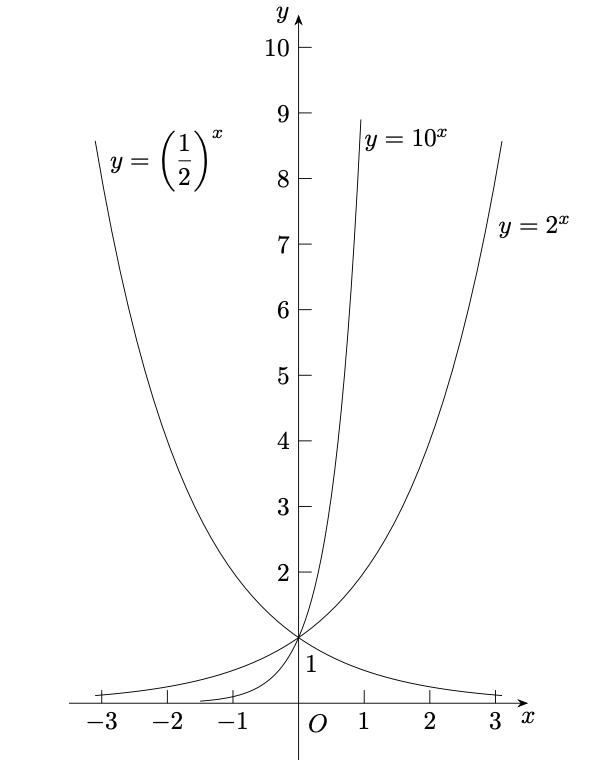
当a>1时的图像特征
- 严格单调递增
- 向上凸
- lim(x→-∞) aˣ = 0
- 过点(0,1)和(1,a)
- 增长速度随x增大而加快
图像形状:从左到右上升,越来越陡
当0<a<1时的图像特征
- 严格单调递减
- 向上凸
- lim(x→∞) aˣ = 0
- 过点(0,1)和(1,a)
- 下降速度随x增大而减缓
图像形状:从左到右下降,逐渐趋近x轴
负指数函数y=-aˣ的特征
- 图像在x轴下方
- 过点(0,-1)和(1,-a)
- x轴仍是水平渐近线
- 当a>1时单调递减
- 值域:所有负实数
指数函数图像的常见误区
- 不要混淆a>1和0<a<1的图像形状
- 记住图像永远不会碰触x轴
- 注意负指数函数与正指数函数的区别
- 不要忘记检查过点(0,1)
- 注意增长/衰减的速率变化
图像应用举例
解法:
- 3ᵃ = 7
- 3ᵇ = 63
- 3ᵇ⁻ᵃ = 63/7 = 9 = 3²
- 所以b-a = 2