函数连续性

连续函数是在定义域内没有间断点、跳跃点或空洞的函数，其函数值随自变量的变化而平滑变化。

连续性定义 $f(x)$ 在点 $x=a$ 处连续需满足三个条件:

1. $f(a)$ 存在（有定义）
2. ${\lim }_{x\to a}f(x)$ 存在
3. ${\lim }_{x\to a}f(x)=f(a)$

例子：$f(x)=x^2$ 在任意点都连续，因为对任意 $a$:

• $f(a)=a^2$ 存在
• ${\lim }_{x\to a}{x}^2$ 存在
• ${\lim }_{x\to a}{x}^2=a^2=f(a)$

间断点类型

1. 可去间断点：左右极限存在且相等，但不等于函数值，或该点函数值不存在
2. 跳跃间断点：左右极限存在但不相等
3. 无穷间断点：至少一侧极限不存在

连续函数的性质

1. 基本初等函数在定义域内连续
2. 连续函数的和、差、积、商(分母不为0)仍连续
3. 复合函数的连续性：外函数和内函数都连续则复合函数连续

例子：$f(x)=\sin (x^2)$ 在 $\mathbb{R}$ 上连续

• $x^2$ 连续
• $\sin x$ 连续
• 它们的复合也连续

闭区间上连续函数的性质

1. 有界性：一定有上下界
2. 最值定理：一定能取到最大值和最小值
3. 介值定理：能取到最值之间的任意值

例子：$f(x)=x^2$ 在 $[0,1]$ 上：

• 有界：$0\le f(x)\le 1$
• 最小值为0，最大值为1
• 能取到 $[0,1]$ 之间任意值

常见误区

1. 分段函数不一定不连续
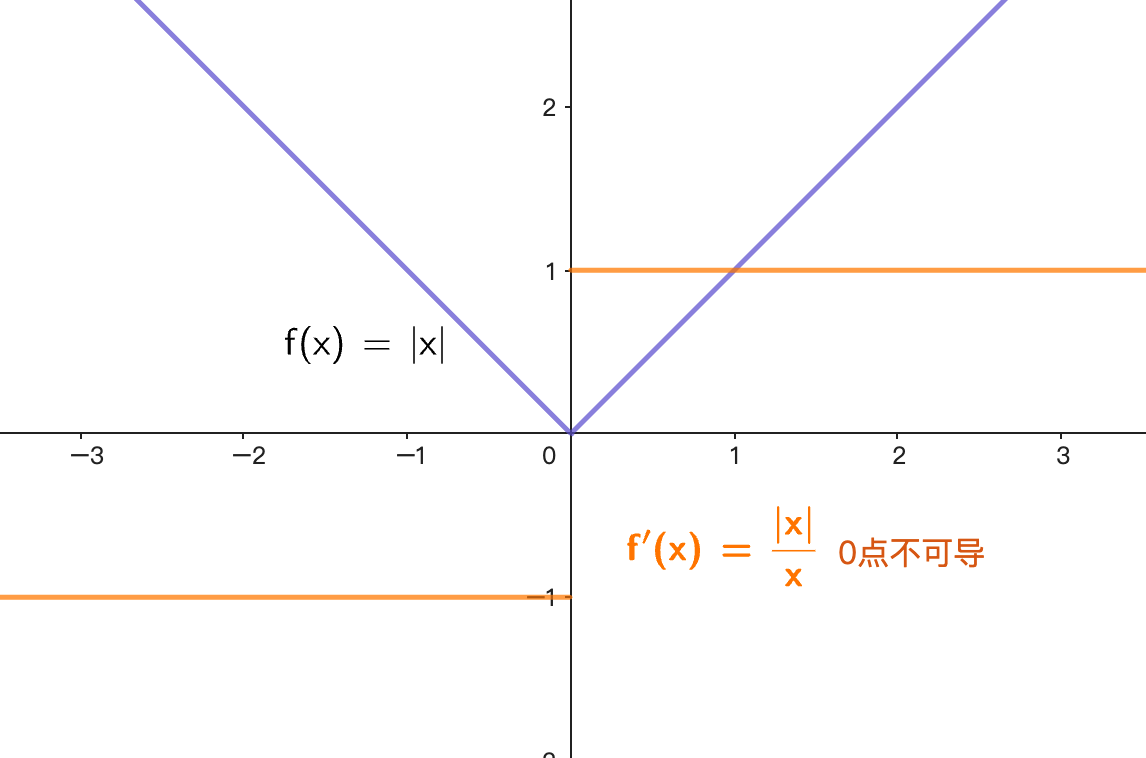
2. 图像有转折点不代表不连续
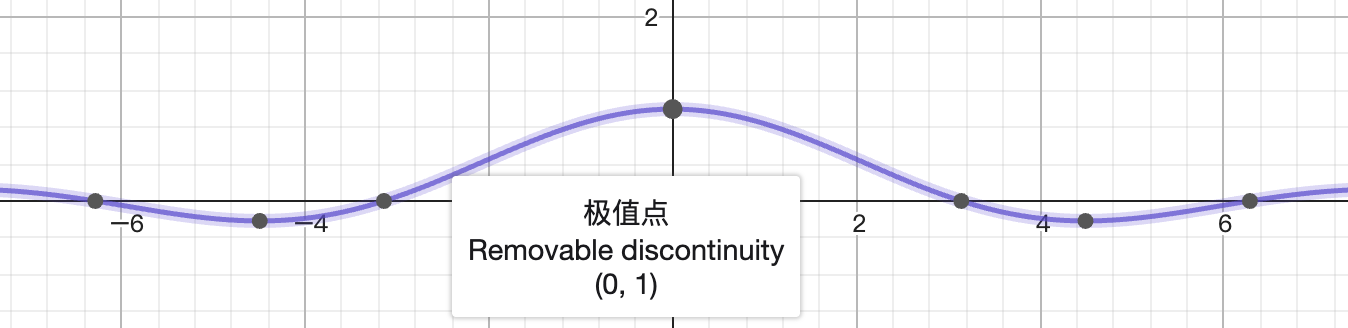
3. 无定义点不一定是间断点

例子：$f(x)=|x|$ 在 $x=0$ 处连续

• 虽然是分段函数
• 虽然在 $x=0$ 处有转折
• 但满足连续性定义