AM-GM不等式

算术几何平均不等式（AM-GM不等式）

内容：对于任意 n 个正实数 $a_1,a_2,...,a_n$，有： $\frac{a_1+a_2+...+a_n}{n}\ge \sqrt[n]{a_1{a}_2...a_n}$ 当且仅当 $a_1=a_2=...=a_n$ 时，等号成立。

二元 AM-GM 不等式

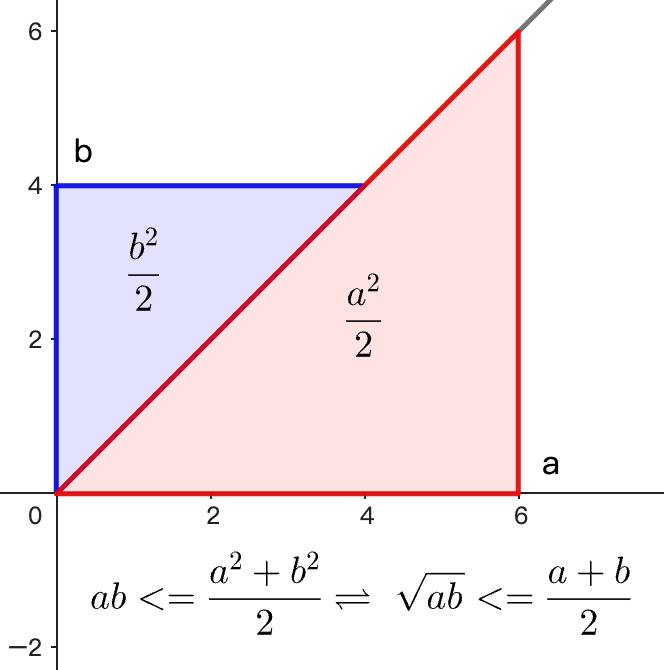
对于任意两个正实数 a 和 b，有： $\frac{a+b}{2}\ge \sqrt{ab}$ 当且仅当 a = b 时，等号成立。

加权 AM-GM 不等式

对于正实数 $a_1,a_2,...,a_n$ 和正权重 $w_1,w_2,...,w_n$，有： $\frac{w_1{a}_1+w_2{a}_2+...+w_n{a}_n}{w_1+w_2+...+w_n}\ge (a_1^{w_1}{a}_2^{w_2}...a_n^{w_n}{)}^{\frac{1}{w_1+w_2+...+w_n}}$

AM-GM 不等式的应用

• 优化问题（最大值/最小值）
• 不等式证明
• 几何问题（如面积最大化）
• 经济学中的效用最大化

AM-GM-HM 不等式

对于正实数 $a_1,a_2,...,a_n$，有： $\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+...+\frac{1}{a_n}}\le \sqrt[n]{a_1{a}_2...a_n}\le \frac{a_1+a_2+...+a_n}{n}$ 其中左边是调和平均数，中间是几何平均数，右边是算术平均数。

常见题型和解法

1. 题型：给定和或积，求另一个的极值 解法：使用 AM-GM 不等式，当所有变量相等时取得极值

已知 $a+b+c=6$，求 $abc$ 的最大值。

解答： $\frac{a+b+c}{3}\ge \sqrt[3]{abc}$ $2\ge \sqrt[3]{abc}$ $abc\le 8$ 当 $a=b=c=2$ 时取得最大值 8。

2. 题型：证明不等式 解法：将不等式转化为 AM-GM 的形式

证明： $\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}$，其中 $a,b>0$

证明： $\frac{1}{a}+\frac{1}{b}\ge 2\sqrt{\frac{1}{ab}}=\frac{2\sqrt{ab}}{ab}$ $\frac{a+b}{2}\ge \sqrt{ab}$ $(a+b{)}^2\ge 4ab$ $\frac{2\sqrt{ab}}{ab}\ge \frac{4}{a+b}$ 因此原不等式成立。

3. 题型：最优化问题 解法：构造合适的表达式，应用 AM-GM 不等式

已知 $x>0$，$y>0$，且 $xy=1$，求 $x+\frac{1}{y}$ 的最小值。

解答： $x+\frac{1}{y}=x+\frac{x}{xy}=x+x=2x$ 由 AM-GM 不等式： $\frac{x+\frac{1}{x}}{2}\ge \sqrt{x\cdot \frac{1}{x}}=1$ 所以 $x+\frac{1}{x}\ge 2$ 当 $x=1$ 时取得最小值 2。

4. 题型：几何优化问题 解法：将几何量转化为代数表达式，应用 AM-GM 不等式

在所有周长为 10 的矩形中，求面积最大的矩形。

解答： 设矩形的长为 x，宽为 y，则： $2x+2y=10$，$x+y=5$ 面积 $S=xy$ 由 AM-GM 不等式： $\frac{x+y}{2}\ge \sqrt{xy}$ $\frac{5}{2}\ge \sqrt{S}$ $S\le (\frac{5}{2}{)}^2=\frac{25}{4}$ 当 $x=y=\frac{5}{2}$ 时，面积最大，为 $\frac{25}{4}$。