算术平均值
两个数a和b的算数平均值定义为,在直线上,对应的点是以a和b为端点的线段的中点。
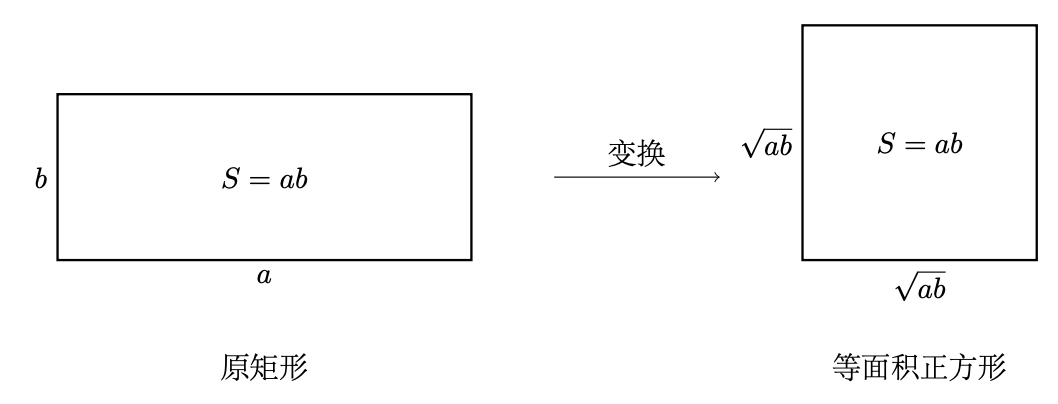
几何平均值
两个非负数a和b的几何平均值时乘积的平方根,计为
从数列角度看AM-GM:
数列角度
- 算数平均数:等差数列
- 几何平均数:等比数列
构造方程
- 算术平均值是一个数,使得
- 几何平均数是一个数,使得
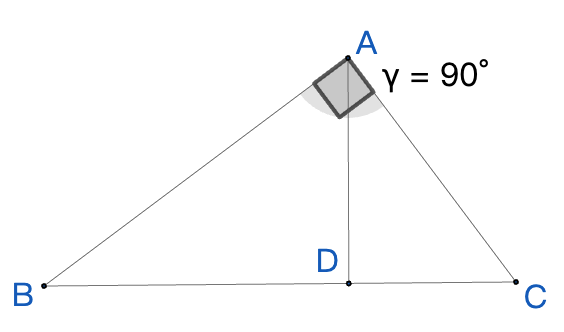
既然算术平均数的意义是两点之间的中点,那么进一步想一想几何平均数的几何意义?
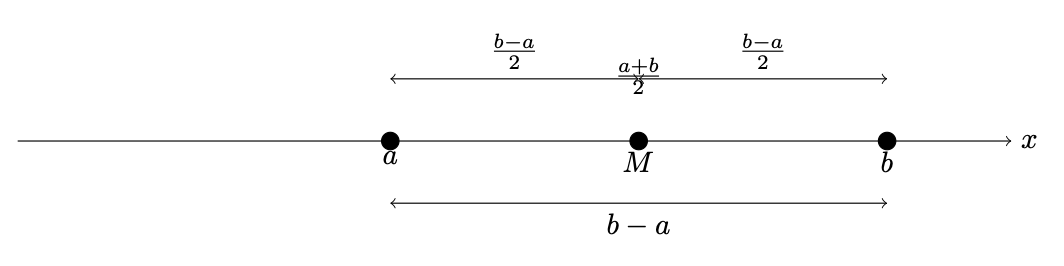
如何证明两个数在直线上的中点是两个数的算数平均值?
1. 不失一般性,假设
2. 两点之间的距离是,距离的一半是
3. 中点是
2. 两点之间的距离是,距离的一半是
3. 中点是