- 收藏内容
- 分享内容
- 添加笔记
- 打印内容
- 提问相关问题
QM-AM 不等式
均方根大于等于算数平均数。
ka12+⋯+ak2fQM≥na1+a2+⋯+an≥fAM
均方根大于等于算数平均数。
ka12+⋯+ak2fQM≥na1+a2+⋯+an≥fAM
AM-GM 不等式
算术平均数 - 几何平均数(AM-GM)不等式描述的是:非负实数的算术平均数大于或等于同一列表的几何平均数;当且仅当列表中的每个数字都相同时,等号成立。
从数学上讲,对于 𝑛 个非负实数 a1,a2,...,an :
na1+a2+⋯+an≥na1a2…an,
算术平均数 - 几何平均数(AM-GM)不等式描述的是:非负实数的算术平均数大于或等于同一列表的几何平均数;当且仅当列表中的每个数字都相同时,等号成立。
从数学上讲,对于 𝑛 个非负实数 a1,a2,...,an :
na1+a2+⋯+an≥na1a2…an,
Quadratic Mean均方根(二次均值)
假设给定的数据是用它们的平方加权的。在这种情况下,我们可以考虑一个均值,它具有这样的特性:k 乘以均值的平方等于各值的平方之和:
kfQM2=a12+⋯+ak2
fQM=ka12+⋯+ak2
假设给定的数据是用它们的平方加权的。在这种情况下,我们可以考虑一个均值,它具有这样的特性:k 乘以均值的平方等于各值的平方之和:
kfQM2=a12+⋯+ak2
fQM=ka12+⋯+ak2
(1⋅a1+1⋅a2+⋯+1⋅an)2a12+a22+⋯+an2≤(a12+a22+⋯+an2)(1+1+⋯+1)≥n(1⋅a1+1⋅a2+⋯+1⋅an)2.
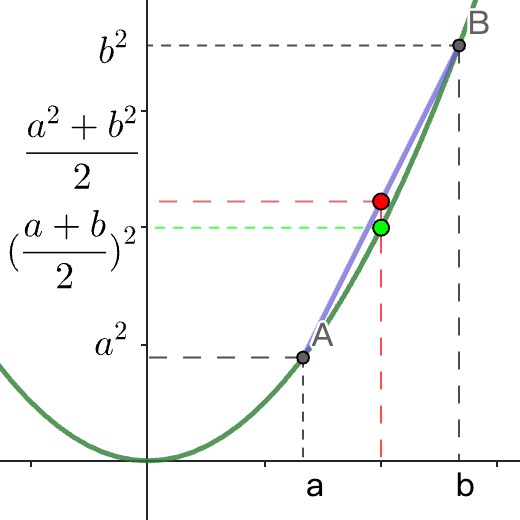
当n=2时:
a12+a222a12+a222a12+a22≥2(a1+a2)2≥4(a1+a2)2≥2a1+a2
当n=2时:
a12+a222a12+a222a12+a22≥2(a1+a2)2≥4(a1+a2)2≥2a1+a2
柯西-施瓦茨不等式
指出对于所有实数序列,我们有
(i=1∑nai2)(i=1∑nbi2)≥(i=1∑naibi)2.
指出对于所有实数序列,我们有
(i=1∑nai2)(i=1∑nbi2)≥(i=1∑naibi)2.