笔记内容
点积的定义
向量点积是向量代数中的基本运算,它将两个向量映射为一个标量。
- 代数定义:
- , 是向量的模长
- 是两个向量之间的夹角 ()
- 坐标定义:
- 二维:
- 三维:
- 一般:
- 结果:点积的结果是一个标量,不是向量
点积的几何意义
- 向量在向量方向上的投影与的乘积
- 即:
- 投影长度:
- 表示一个向量在另一个向量方向上的”有效分量”
点积的性质
- 交换律:
- 分配律:
- 标量结合律:
- 自身点积:
- 零向量点积:
特殊情况
- 正交向量: 当且仅当 或其中一个为零向量
- 同向向量: 当且仅当 和 方向相同
- 反向向量: 当且仅当 和 方向相反
点积的应用
计算向量夹角
- 可用于判断两向量的关系:
- :锐角 ()
- :直角 ()
- :钝角 ()
向量投影
- 向量在向量方向上的投影:
- 投影向量:
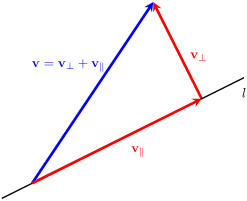
正交分解
- 任意向量可分解为平行于和垂直于的两个分量:
- 平行分量:
- 垂直分量:
物理应用
- 功的计算:
- 是力, 是位移
- 只有力在位移方向上的分量做功
- 电功率:(电场与电流密度的点积)
- 力矩:判断力是否产生转动效果
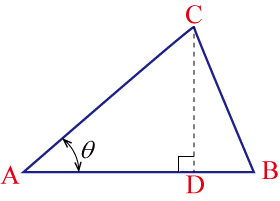
点积与余弦定理的关系
- 余弦定理:
- 向量形式:
- 其中
关键词与符号
- 点积 (Dot product)
- 内积 (Inner product)
- 标量积 (Scalar product)
- 投影 (Projection)
- 正交 (Orthogonal)
- 夹角 (Angle)
- 余弦定理 (Law of cosines)
- 方向余弦 (Direction cosines)
- 正交分解 (Orthogonal decomposition)
- ,
核心问题
- 什么是向量点积?它的几何意义是什么?
- 如何计算两个向量的点积?
- 点积有哪些重要性质?
- 点积与向量投影有什么关系?
- 点积在物理学和工程中有哪些应用?
- 如何利用点积判断两个向量的关系?
总结
向量点积是向量代数中的基本运算,它将两个向量映射为一个标量。点积的代数定义是 ,坐标表示为各对应分量乘积之和。
几何上,点积表示一个向量在另一个向量方向上的投影与后者模长的乘积,反映了两个向量在方向上的”相似程度”。
点积满足交换律、分配律和标量结合律等代数性质。通过点积可以计算向量间的夹角、判断向量的正交性、进行向量的正交分解,以及计算一个向量在另一个向量方向上的投影。
在物理学中,点积用于计算功、电功率等物理量;在计算机图形学中,点积用于光照模型、碰撞检测等应用。点积与余弦定理有密切关系,提供了从几何到代数的重要联系
理解点积的本质和应用,对于掌握向量代数、解决物理和工程问题具有重要意义。点积将几何直观与代数计算完美结合,为我们提供了处理向量关系的强大工具。