向量的坐标表示可以看成是从原点出发到坐标点的标准向量,或者看成,方向上的位移。
向量的表示
表示方法
两种表示方法
- 两点表示:
- 起点A
- 终点B
- 记作
- 坐标表示(分量表示):
- 向量
- 其中
行列式
线性运算更方便: 列向量: 行向量:
转换关系(头尾公式)
点表示→坐标表示:
坐标表示→ 两点表示:
- 任选起点
- 终点为
- 表示同一个向量
理解与分析
坐标表示的原点视角
- 向量可以理解为:
- 从原点出发
- 到达点的位移
- 即,其中O是原点
- 向量的”标准位置”:
- 起点在原点
- 终点即坐标值
- 所有向量都可以移到这个位置
- 几何意义:
- 向量是从原点出发的”箭头”
- 坐标就是终点位置
- 体现了位置和位移的统一
本质联系
- 位移观点:
- 点表示强调起点到终点的移动
- 坐标表示强调移动的量
- 等价性:
- 同一向量可有无数点表示
- 但只有一个坐标表示
- 体现了向量的平移不变性
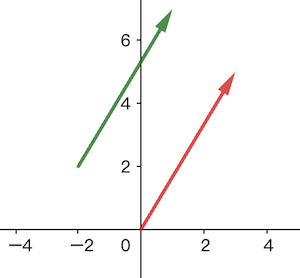
两点表示
坐标表示
params:
- {name: startX, value: 3, min: 0, max: 8}
- {name: startY, value: 2, min: 0, max: 8}
- {name: endX, value: 6, min: 0, max: 8}
- {name: endY, value: 6, min: 0, max: 8}
calcs:
vectorLength: "(sqrt((params.endX - params.startX)^2 + (params.endY - params.startY)^2))"
vectorDx: "params.endX - params.startX"
vectorDy: "params.endY - params.startY"
layout:
OneGraph:
title: 可拖动向量示例
subtitle: 拖动蓝色和红色点来改变向量的起点和终点
graph:
xAxis:
min: 0
max: 10
title: x轴
yAxis:
min: 0
max: 10
title: y轴
grid: true
objects:
# 起点(蓝色点)
- Point:
coordinates: [params.startX, params.startY]
color: blue
size: 2
draggable: true
label: 起点
# 终点(红色点)
- Point:
coordinates: [params.endX, params.endY]
color: red
size: 2
draggable: true
label: 终点
# 向量(箭头)
- Arrow:
begin: [params.startX, params.startY]
end: [params.endX, params.endY]
color: green
width: 3
label: 向量v
# 向量(箭头)
- Arrow:
begin: [0, 0]
end: [params.endX-params.startX, params.endY-params.startY]
color: red
width: 3
label: 向量v
- Label:
coordinates: [6, 3]
text: "`向量v =(${calcs.vectorDx},${calcs.vectorDy})`"
- Label:
coordinates: [6, 4]
text: "`|v| = ${calcs.vectorLength}`"
card
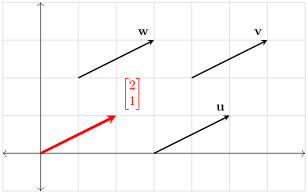
将如图的向量表示为分量形式:

头尾公式:

提示
头尾公式:
