线段外分点的位置向量

概念定义

线段外分点的位置向量是指线段延长线上任意一点的位置向量，可以通过线段两端点的位置向量按特定比例线性组合得到。

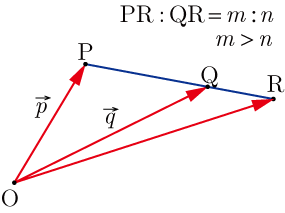
给定线段AB，A点位置向量为$\vec{a}$，B点位置向量为$\vec{b}$，则线段延长线上任意外分点P的位置向量$\vec{p}$可表示为： $\vec{p}=\frac{m\vec{b}-n\vec{a}}{m-n}$

其中m和n是正实数，表示AP:PB = m:n的比例关系。特别地，当m=n时，P点不存在（因为分母为0）。

通俗理解

线段外分点的位置向量就像是在一条绳子的延长线上找点！它告诉我们：如果知道线段两端点的位置，如何找到线段延长线上任意比例位置的点。比如，要找到线段延长线上距离一端2倍长度的点，或者距离一端3倍长度的点，都可以用这个公式轻松计算。这个公式把几何问题转化为代数计算，让我们能精确地”延伸”线段，是向量几何中的一把延伸尺子！

形象记忆

想象你在玩一个”延伸绳子”的游戏：

• 你站在A点，朋友站在B点
• 你们之间拉着一根绳子
• 现在要把绳子向两端延长
• 如果知道延长点距离A点是绳子总长的2倍，距离B点是1倍
• 那么延长点的位置就可以用这个公式精确计算出来

这个公式就像是一个”延伸尺”，帮助我们在线段延长线上精确定位任意比例的点。记住：比例大的那端延伸得更远，就像橡皮筋，拉得越长，延伸得越远！

核心概念

• 位置向量：表示点在空间中的位置的向量
• 外分点：位于线段延长线上的点
• 比例关系：表示点到线段两端距离的比值
• 线性组合：向量的加权和
• 参数方程：用参数表示点的位置
• 向量运算：向量的加法和数乘
• 方向性：外分点的位置与比例关系有关

逻辑结构

线段外分点位置向量的逻辑体系：

1. 基本公式（核心）：

• $\vec{p}=\frac{m\vec{b}-n\vec{a}}{m-n}$

• 其中AP:PB = m:n

2. 特殊情况（应用）：

• 当m>n时，P点在B点外侧

• 当m<n时，P点在A点外侧

• 当m=n时，P点不存在（分母为0）

3. 参数表示（推广）：

• $\vec{p}=(1-t)\vec{a}+t\vec{b}$（t<0或t>1）

• 其中t = m/(m-n)

4. 性质（延伸）：

• 当m>n时，P点更远离A点
• 当m<n时，P点更远离B点
• 当m=n时，P点不存在
• 当m=0时，P点与A点重合
• 当n=0时，P点与B点重合

图解思维

解决外分点问题的思维链：

1. 确定已知条件 → 两端点位置向量和比例关系
2. 选择合适公式 → 根据问题特点选择基本公式或特殊情况
3. 代入计算 → 将已知值代入公式
4. 验证结果 → 检查比例关系是否正确
5. 应用结果 → 用于后续计算或证明

例如：求线段AB延长线上距离A点2倍长度的点的位置向量 思路：AP:PB = 2:1 使用公式：$\vec{p}=\frac{\vec{b}-2\vec{a}}{-1}=2\vec{a}-\vec{b}$

易错提醒

• 误区一：混淆比例方向（AP:PB与PA:PB的区别）
• 误区二：忘记分母（m-n）的归一化
• 误区三：比例值取错（注意比例是距离的比值）
• 边界情况：当m=n时的特殊情况（分母为0）
• 常见错误：在三维空间中忽略某个坐标分量
• 应用陷阱：在参数方程中t的范围控制

提示：画图辅助理解，明确比例关系，注意向量方向

概念意义

线段外分点的位置向量体现了数学中”延伸”与”比例”的统一。它将几何中的比例关系转化为代数中的向量运算，展示了数学不同分支之间的内在联系。

从哲学角度看，这个概念体现了”有限与无限”的关系：通过有限线段的信息，我们可以确定无限延长线上任意点的位置，显示了数学的预测能力。

在实际应用中，这个概念广泛应用于：

• 计算机图形学中的射线计算
• 物理学中的力的分解
• 工程学中的结构设计
• 地理信息系统中的位置计算

掌握这个概念，不仅有助于理解向量几何，还能培养空间思维能力和比例关系分析能力。

极简示例

问：已知线段AB，A点坐标为(1,2)，B点坐标为(5,6)，求线段延长线上距离A点2倍长度的点的坐标。

解：

1. 确定比例关系：AP:PB = 2:1

2. 使用外分点公式： $\vec{p}=\frac{\vec{b}-2\vec{a}}{-1}=2\vec{a}-\vec{b}$

3. 代入坐标： P点x坐标 = 2×1 - 5 = -3 P点y坐标 = 2×2 - 6 = -2

所以，所求点的坐标为(-3, -2)

验证：可以计算AP和PB的距离，验证比例关系是否正确。