任何向量通过归一化为单位向量,它保留了向量的方向信息而统一了大小,是向量和三角函数的桥梁。
单位向量
单位向量的定义
单位向量是长度(模)为1的向量:
给定向量,除以模长,得到归一化后的单位向量:
特点:
- 与原向量方向相同
- 大小为1
- 常用帽子符号(^)表示
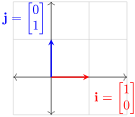
标准单位向量
- 或
- 或
- 或
性质:相互正交且长度为1(正交归一化)
计算示例
求向量的单位向量:
- 计算模长:
- 单位化:
向量分解
优点:
- 分离方向和大小
- 便于计算和分析
- 简化向量运算
注意事项
- 单位向量的点积:
- 计算时注意:
- 不要忘记归一化
- 保持方向不变
- 检查模长是否为1
二维空间标准单位向量
关键词与符号
- 单位向量 (Unit vector)
- 模长 (Magnitude)
- 归一化 (Normalization)
- 方向 (Direction)
- 标准化 (Standardization)
- 单位长度 (Unit length)
- 向量
- 单位向量 或
- 向量范数
核心问题
- 什么是单位向量?为什么需要单位向量?
- 如何将任意非零向量转化为单位向量?
- 单位向量在物理和几何中有什么重要应用?
- 常见坐标系中的标准单位向量是什么?
- 单位向量与向量投影有什么关系?
关联概念