向量叉积

1. 大小等于 $|\vec{a}||\vec{b}|\sin \theta$，其中 $\theta$ 是两向量间的夹角
2. 方向垂直于 $\vec{a}$ 和 $\vec{b}$ 所在平面
3. 方向由右手法则确定：右手四指从 $\vec{a}$ 转向 $\vec{b}$，拇指指向叉积方向

代数公式（三维空间）： 若 $\vec{a}=⟨a_1,a_2,a_3⟩$ 和 $\vec{b}=⟨b_1,b_2,b_3⟩$，则： $\vec{a}\times \vec{b}=⟨a_2{b}_3-a_3{b}_2,a_3{b}_1-a_1{b}_3,a_1{b}_2-a_2{b}_1⟩$

行列式形式： $\vec{a}\times \vec{b}=\left|\begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|$

展开为： $\vec{a}\times \vec{b}=(a_2{b}_3-a_3{b}_2)\vec{i}-(a_1{b}_3-a_3{b}_1)\vec{j}+(a_1{b}_2-a_2{b}_1)\vec{k}$

二维向量的叉积： 若 $\vec{a}=⟨a_1,a_2,0⟩$ 和 $\vec{b}=⟨b_1,b_2,0⟩$，则： $\vec{a}\times \vec{b}=⟨0,0,a_1{b}_2-a_2{b}_1⟩=(a_1{b}_2-a_2{b}_1)\vec{k}$

大小：$|\vec{a}\times \vec{b}|=|\vec{a}||\vec{b}|\sin \theta$

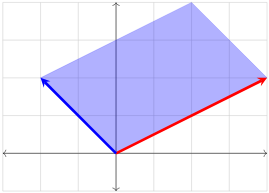
1. 表示由 $\vec{a}$ 和 $\vec{b}$ 构成的平行四边形的面积
2. 当 $\vec{a}$ 和 $\vec{b}$ 平行时，$\sin \theta =0$，叉积为零向量
3. 当 $\vec{a}$ 和 $\vec{b}$ 垂直时，$\sin \theta =1$，叉积大小达到最大值 $|\vec{a}||\vec{b}|$

方向：垂直于 $\vec{a}$ 和 $\vec{b}$ 所在平面

1. 遵循右手法则
2. 形成右手坐标系：$\vec{a}$、$\vec{b}$ 和 $\vec{a}\times \vec{b}$

平行四边形面积：

1. 由向量 $\vec{a}$ 和 $\vec{b}$ 构成的平行四边形面积为 $|\vec{a}\times \vec{b}|$

三角形面积：

1. 由向量 $\vec{a}$ 和 $\vec{b}$ 构成的三角形面积为 $\frac{1}{2}|\vec{a}\times \vec{b}|$
2. 由三点 $P$、$Q$ 和 $R$ 构成的三角形面积：$A=\frac{1}{2}|\overrightarrow{PQ}\times \overrightarrow{PR}|$

反交换律：$\vec{a}\times \vec{b}=-(\vec{b}\times \vec{a})$

1. 交换向量顺序，叉积方向相反

不满足结合律：$(\vec{a}\times \vec{b})\times \vec{c}\ne \vec{a}\times (\vec{b}\times \vec{c})$

1. 叉积不是结合的，括号位置很重要

分配律：

1. $\vec{a}\times (\vec{b}+\vec{c})=\vec{a}\times \vec{b}+\vec{a}\times \vec{c}$
2. $(\vec{a}+\vec{b})\times \vec{c}=\vec{a}\times \vec{c}+\vec{b}\times \vec{c}$

标量乘法：

1. $(\alpha \vec{a})\times \vec{b}=\alpha (\vec{a}\times \vec{b})=\vec{a}\times (\alpha \vec{b})$，其中 $\alpha$ 是标量

自叉积为零：$\vec{a}\times \vec{a}=\vec{0}$

1. 任何向量与自身的叉积都是零向量

与零向量的叉积：$\vec{a}\times \vec{0}=\vec{0}\times \vec{a}=\vec{0}$