向量问题

已知 $△ABC$ 是边长为 2 的等边三角形， D是AC上的点， $\overrightarrow{AD}=2\overrightarrow{DC}$, E是AB的中点， BD与CE交于点 O ，那么（ ）

A． $\overrightarrow{OE}+\overrightarrow{OC}=0$ B． $\overrightarrow{AB}\cdot \overrightarrow{CE}=-1$ C． $|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}|=\frac{\sqrt{3}}{2}\mathrm{D}$ D． $|\overrightarrow{DE}|=\frac{\sqrt{13}}{3}$

---

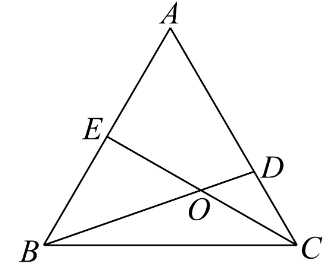
首先建立坐标系，然后计算各点坐标，最后验证各选项。

1. 建立坐标系

取A为原点，AB沿x轴正方向，则可以设：

• A(0, 0)
• B(2, 0)
• C(1, $\sqrt{3}$) (根据等边三角形的性质)

2. 计算D点坐标

已知D在AC上且$\overrightarrow{AD}=2\overrightarrow{DC}$，这意味着D将AC分为2:1的比例，即： $D=A+\frac{2}{3}(C-A)=\frac{2}{3}C+\frac{1}{3}A$

代入坐标： $D=\frac{2}{3}(1,\sqrt{3})+\frac{1}{3}(0,0)=(\frac{2}{3},\frac{2\sqrt{3}}{3})$

3. 计算E点坐标

E是AB的中点，所以： $E=\frac{A+B}{2}=\frac{(0,0)+(2,0)}{2}=(1,0)$

4. 计算O点坐标

O是BD与CE的交点。我们可以通过参数方程求解：

BD的参数方程：$(1-t)B+tD=(1-t)(2,0)+t(\frac{2}{3},\frac{2\sqrt{3}}{3})$

CE的参数方程：$(1-s)C+sE=(1-s)(1,\sqrt{3})+s(1,0)$

令两者相等，可得： $(2-2t+\frac{2t}{3},\frac{2t\sqrt{3}}{3})=(1,(1-s)\sqrt{3})$

这给出： $2-2t+\frac{2t}{3}=1$ $\frac{2t\sqrt{3}}{3}=(1-s)\sqrt{3}$

从第一个方程得：$t=\frac{3}{4}$

从第二个方程得：$s=1-\frac{2t}{3}=1-\frac{2\cdot \frac{3}{4}}{3}=1-\frac{1}{2}=\frac{1}{2}$

将t代入BD的参数方程，得到O点坐标： $O=(1-\frac{3}{4})(2,0)+\frac{3}{4}(\frac{2}{3},\frac{2\sqrt{3}}{3})=(\frac{1}{2},0)+(\frac{1}{2},\frac{\sqrt{3}}{2})=(1,\frac{\sqrt{3}}{2})$

5. 验证选项

选项A：$\overrightarrow{OE}+\overrightarrow{OC}=0$

$\overrightarrow{OE}=E-O=(1,0)-(1,\frac{\sqrt{3}}{2})=(0,-\frac{\sqrt{3}}{2})$ $\overrightarrow{OC}=C-O=(1,\sqrt{3})-(1,\frac{\sqrt{3}}{2})=(0,\frac{\sqrt{3}}{2})$

因此，$\overrightarrow{OE}+\overrightarrow{OC}=(0,-\frac{\sqrt{3}}{2})+(0,\frac{\sqrt{3}}{2})=(0,0)=0$

选项A正确。

选项B：$\overrightarrow{AB}\cdot \overrightarrow{CE}=-1$

$\overrightarrow{AB}=B-A=(2,0)-(0,0)=(2,0)$ $\overrightarrow{CE}=E-C=(1,0)-(1,\sqrt{3})=(0,-\sqrt{3})$

$\overrightarrow{AB}\cdot \overrightarrow{CE}=2\cdot 0+0\cdot (-\sqrt{3})=0$

选项B不正确。

选项C：$|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}|=\frac{\sqrt{3}}{2}$

$\overrightarrow{OA}=A-O=(0,0)-(1,\frac{\sqrt{3}}{2})=(-1,-\frac{\sqrt{3}}{2})$ $\overrightarrow{OB}=B-O=(2,0)-(1,\frac{\sqrt{3}}{2})=(1,-\frac{\sqrt{3}}{2})$ $\overrightarrow{OC}=C-O=(1,\sqrt{3})-(1,\frac{\sqrt{3}}{2})=(0,\frac{\sqrt{3}}{2})$

$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=(-1,-\frac{\sqrt{3}}{2})+(1,-\frac{\sqrt{3}}{2})+(0,\frac{\sqrt{3}}{2})=(0,-\frac{\sqrt{3}}{2})$

$|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}|=\sqrt{0^2+(-\frac{\sqrt{3}}{2}{)}^2}=\frac{\sqrt{3}}{2}$

选项C正确。

选项D：$|\overrightarrow{DE}|=\frac{\sqrt{13}}{3}$

$\overrightarrow{DE}=E-D=(1,0)-(\frac{2}{3},\frac{2\sqrt{3}}{3})=(\frac{1}{3},-\frac{2\sqrt{3}}{3})$

$|\overrightarrow{DE}|=\sqrt{(\frac{1}{3}{)}^2+(-\frac{2\sqrt{3}}{3}{)}^2}=\sqrt{\frac{1}{9}+\frac{12}{9}}=\sqrt{\frac{13}{9}}=\frac{\sqrt{13}}{3}$

选项D正确。

答案

根据以上分析，选项A、C和D都是正确的。