点积知识卡片

代数定义：

• a·b = x₁x₂ + y₁y₂ + z₁z₂

几何定义：

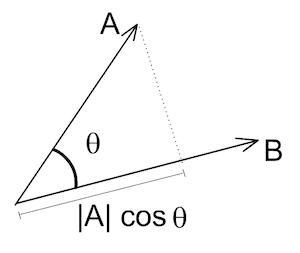
• a·b = |a||b|cosθ
• θ是两向量夹角

1. 投影关系：

   1. 点积 = 一个向量在另一个向量上的投影长度 × 被投影向量的长度

2. 基本性质：

   1. 交换律：a·b = b·a
   2. 分配律：a·(b+c) = a·b + a·c
   3. 结合律：(ka)·b = k(a·b)

3. 特殊情况：

   1. 垂直时点积为0
   2. 同向时点积最大
   3. 反向时点积最小

1. 物理应用：

   1. 功的计算：W = F·s
   2. 力的分解
   3. 电场通量

2. 计算机图形：

   1. 光照模型
   2. 碰撞检测
   3. 视角计算

3. 信号处理：

   1. 相关性计算
   2. 信号匹配
   3. 特征提取

1. 度量本质：

   1. 提供了向量间关系的度量方式
   2. 统一了代数和几何的观点
   3. 体现了空间的内积结构

2. 不变性：

   1. 与坐标系选择无关
   2. 保持旋转变换不变
   3. 反映本质几何关系

数学内部联系：

• 线性代数（内积空间）
• 解析几何（投影、夹角）
• 微积分（方向导数）

跨学科联系：

• 物理学（功、能量）
• 信号处理（相关性）
• 机器学习（相似度计算）
• 计算机图形学（渲染）

1. AI/机器学习：

   1. 余弦相似度
   2. 神经网络计算
   3. 特征向量匹配

2. 图形技术：

   1. 3D建模
   2. VR/AR场景
   3. 游戏物理引擎

3. 数据科学：

   1. 相关性分析
   2. 降维处理
   3. 聚类算法