card
基础计算类题型有哪些?
考虑基本定义和性质
- 直接计算型:
已知a=(1,2,3), b=(2,-1,4),求a·b
解法:
a·b = 1×2 + 2×(-1) + 3×4
= 2 - 2 + 12
= 12
- 夹角计算型:
已知|a|=2, |b|=3, a·b=3,求向量夹角
解法:
cosθ = (a·b)/(|a||b|)
= 3/(2×3)
= 1/2
θ = 60°
提示
考虑基本定义和性质
card
几何证明类题型有哪些?
考虑几何关系的证明
- 垂直证明型:
证明:若a·b=0,则a⊥b
证明:
a·b = |a||b|cosθ = 0
由于|a|≠0, |b|≠0
所以cosθ=0
因此θ=90°,即a⊥b
- 三角形性质证明:
证明:在三角形ABC中,若a²+b²=c²,则∠C=90°
证明:
设a,b,c为对应边的向量
则c=a-b
c²=(a-b)·(a-b)=a²+b²-2a·b
已知a²+b²=c²
代入得:2a·b=0
因此∠C=90°
提示
考虑几何关系的证明
card
物理应用类题型有哪些?
考虑力学和能量计算
- 功的计算:
一个力F=(3,4,0)N沿位移s=(2,2,0)m移动,求功
解法:
W = F·s
= 3×2 + 4×2 + 0×0
= 14 焦耳
- 力的分解:
一个力F=10N,与水平面夹角30°,求水平和竖直分力
解法:
Fx = F·i = 10cos30° = 8.66N
Fy = F·j = 10sin30° = 5N
提示
考虑力学和能量计算
card
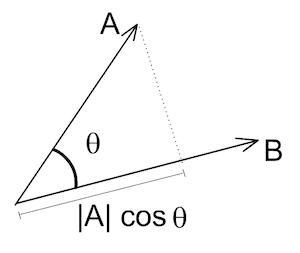
投影应用类题型有哪些?
考虑向量投影的计算
- 投影长度计算:
求向量a=(1,2,2)在b=(2,0,1)上的投影长度
解法:
proj_b a = (a·b)/|b|
= (1×2 + 2×0 + 2×1)/√5
= 4/√5
- 投影向量计算:
求向量a=(3,4)在x轴上的投影向量
解法:
i=(1,0)
proj_i a = ((a·i)/|i|²)i
= (3×1 + 4×0)×(1,0)
= (3,0)
提示
考虑向量投影的计算
card
最值问题类题型有哪些?
考虑点积的极值特性
- 点积最大值问题:
已知|a|=2, |b|=3,求a·b的最大值
解法:
|a·b| ≤ |a||b|
a·b = |a||b|cosθ
最大值在θ=0°时取得
max(a·b) = 2×3 = 6
- 方向最优化问题:
已知力F=(3,4),求单位向量u,使F·u最大
解法:
F·u = |F|cosθ
当u与F同向时最大
u = F/|F| = (3/5, 4/5)
最大值为5
提示
考虑点积的极值特性
card
参数问题类题型有哪些?
考虑含参数的点积方程
- 参数确定问题:
若向量a=(k,1), b=(1,k)垂直,求k的值
解法:
a·b = 0
k×1 + 1×k = 0
2k = 0
k = 0
- 参数范围问题:
已知|a|=1,对于任意|b|=1,若a·b ≥ m,求m的最小值
解法:
a·b = cosθ
-1 ≤ cosθ ≤ 1
所以m的最小值为-1
提示
考虑含参数的点积方程
card
距离计算类题型有哪些?
考虑点到直线、平面的距离
- 点到直线距离:
求点P(1,2,3)到直线l: r=t(2,0,1)的距离
解法:
设A(0,0,0)为直线上一点
AP=(1,2,3)
d = |AP×l|/|l|
= |AP|sinθ
= |AP|√(1-(AP·l)²/(|AP|²|l|²))
- 点到平面距离:
求点P(1,1,1)到平面2x+2y+z=6的距离
解法:
平面法向量n=(2,2,1)
d = |2×1 + 2×1 + 1×1 - 6|/√(2² + 2² + 1²)
= |5 - 6|/3
= 1/3
提示
考虑点到直线、平面的距离
card
向量分解类题型有哪些?
考虑向量在不同基下的分解
- 正交基分解:
将向量a=(2,2)分解为两个正交向量u=(1,1)和v=(1,-1)的线性组合
解法:
a = ku + mv
k = (a·u)/(u·u) = 4/2 = 2
m = (a·v)/(v·v) = 0/2 = 0
因此a = 2u + 0v = 2(1,1)
- 非正交基分解:
将向量a=(3,3)分解到u=(2,0)和v=(1,2)下
解法:
设a = xu + yv
得方程组:
2x + y = 3
2y = 3
解得:x = 1, y = 3/2
提示
考虑向量在不同基下的分解