平滑函数是比函数连续性具有更强性质的函数类型,主要涉及导数的存在性和连续性。
基本概念对比
性质 连续函数 平滑函数 定义 函数值连续变化 所有阶导数都存在且连续 图像特征 无间断 无尖点、无角点 数学符号
典型函数举例
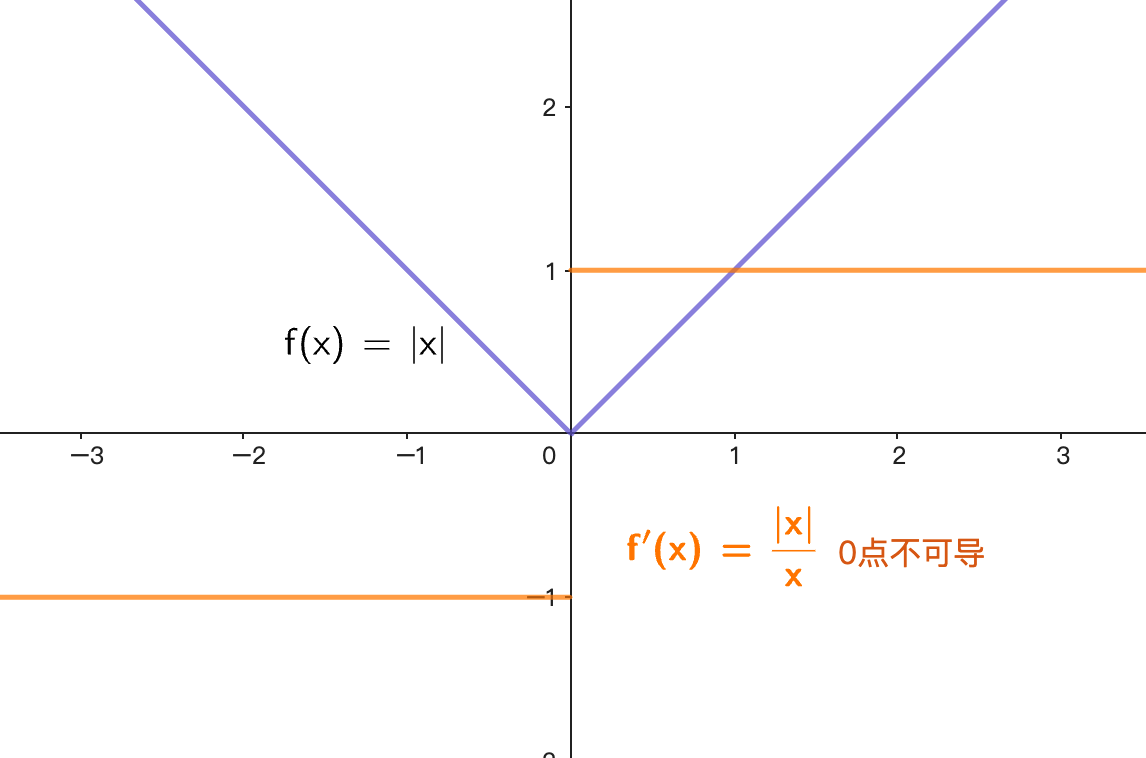
- 连续但不平滑:
- (在x=0处不可导)
- (在x=0处导数无穷大)
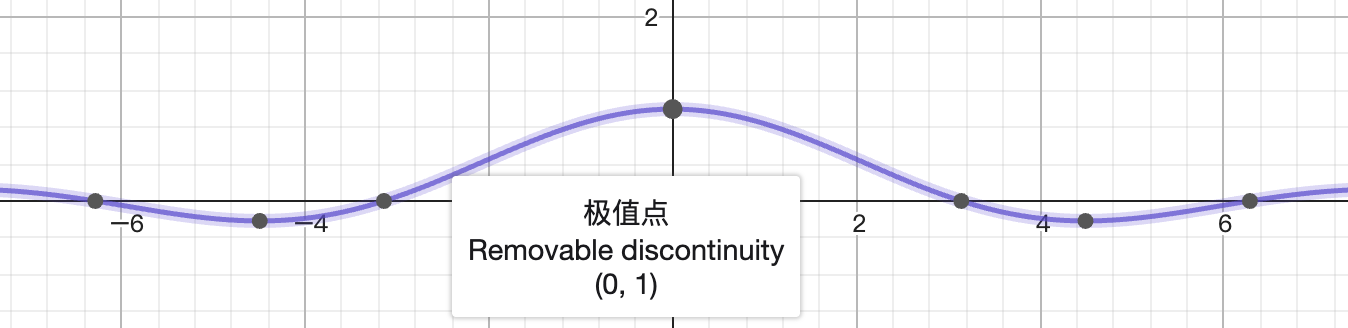
- 平滑函数:
平滑度等级
- :连续函数
- :一阶导数连续
- :二阶导数连续
- :k阶导数连续
- :无限次可导
应用场景
- 物理学:
- 运动轨迹
- 场的分布
- 工程学:
- 曲线设计
- 数值计算
- 计算机图形学:
- 贝塞尔曲线
- 样条函数
重要性质
- 平滑函数的性质:
- 可以进行泰勒展开
- 便于数值计算
- 物理过程更自然
- 平滑化处理:
- 数据平滑
- 噪声过滤
- 插值方法
- 局限性:
- 不能描述突变现象
- 计算复杂度高
- 可能过度简化
.png)
