几何平均数

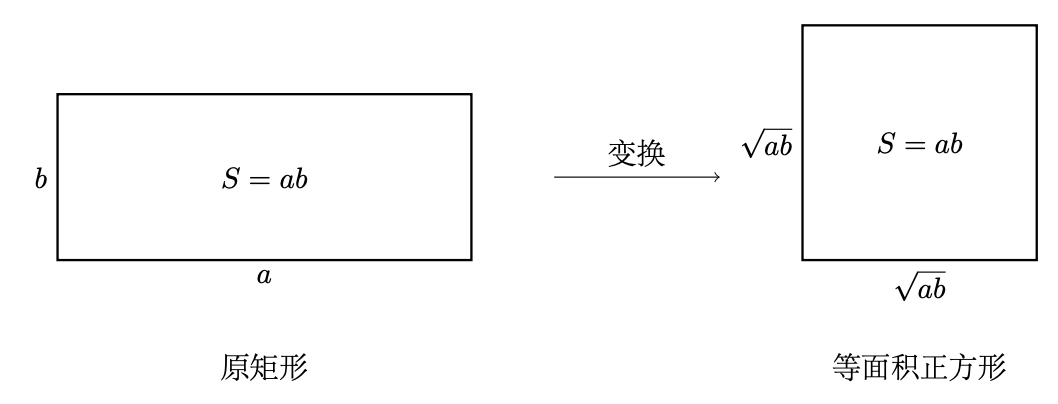
几何平均数的定义

几何平均数是一种幂平均数，对于正实数集合{a₁, a₂, …, aₙ}，其几何平均数为：

$GM(a_1,...,a_n)=\sqrt[n]{a_1{a}_2...a_n}$

例如：

• $GM(4,9)=\sqrt{4\cdot 9}=\sqrt{36}=6$
• $GM(8,27,64)=\sqrt[3]{8\cdot 27\cdot 64}=24$

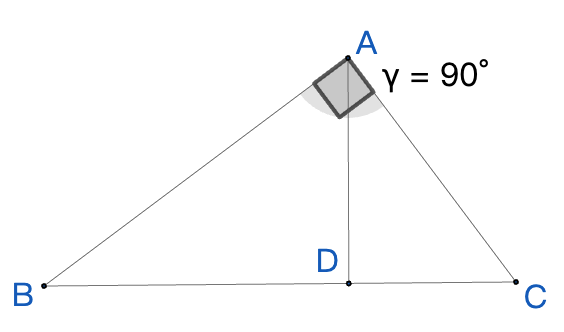
几何意义 在直角三角形中：

1. 如果直角边长度为a和b
2. 则高线将斜边分成两段
3. 高线长度$h=\sqrt{ab}$
4. 即高线长度是两段斜边长度的几何平均数

这就是”几何平均数”名称的由来

重要性质

1. 对数性质： 通过取对数，我们有 $\log \text{GM}(a_1,\cdots ,a_n)=\log \sqrt[n]{a_1{a}_2\cdots a_n}=\frac{\log a_1+\log a_2+\cdots +\log a_n}{n}.$

• 几何平均数的对数等于对数的算术平均数

2. 不等式关系：

• AM ≥ GM（算术-几何平均不等式）
• (a+b)/2 ≥ √ab
• 当且仅当所有数相等时取等号