差集

差集（Set Difference）是一个重要的集合运算概念，表示属于集合 A 但不属于集合 B 的所有元素组成的集合。

定义

• 设有两个集合 A 和 B
• A 与 B 的差集（记作 A - B 或 A \ B）
• 表示属于集合 A 但不属于集合 B 的所有元素组成的集合

数学表达式

$A-B=\{x|x\in A\text{且}x\notin B\}$

示例

1. 如果 A = {1, 2, 3, 4, 5}，B = {4, 5, 6, 7} 则 A - B = {1, 2, 3}

2. 如果 A = {a, b, c, d}，B = {b, d, e, f} 则 A - B = {a, c}

重要性质

1. A - B ≠ B - A（差集不满足交换律）
2. A - ∅ = A（与空集的差集是自身）
3. A - A = ∅（与自身的差集是空集）
4. 如果 A ⊆ B，则 A - B = ∅

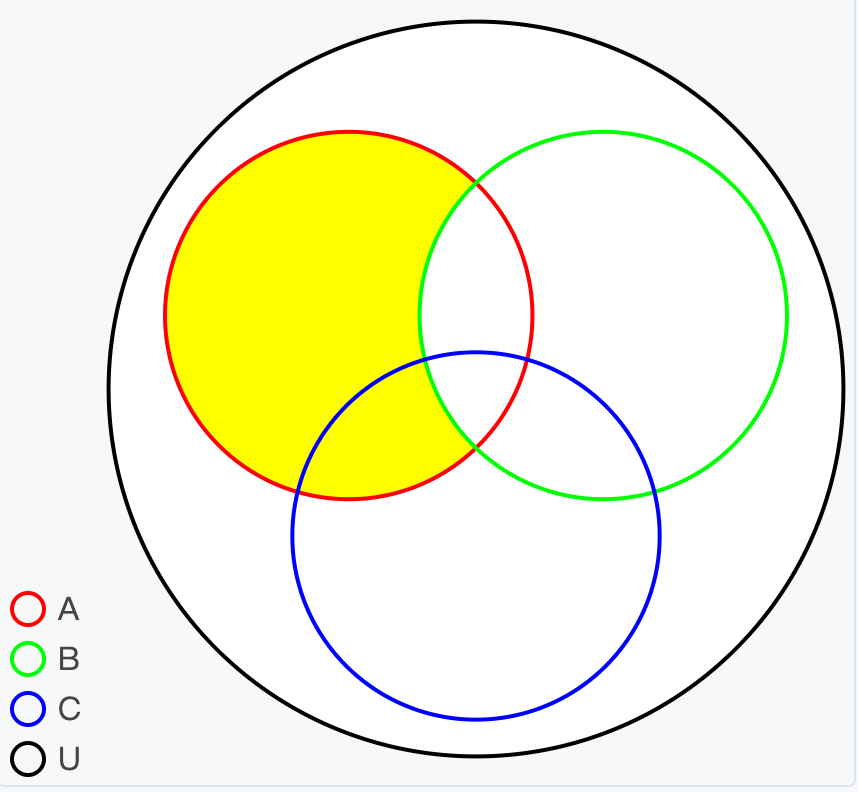
可以用文氏图直观地表示差集：

• A - B 在图中表现为只属于 A 的那部分区域（不包括与 B 重叠的部分）