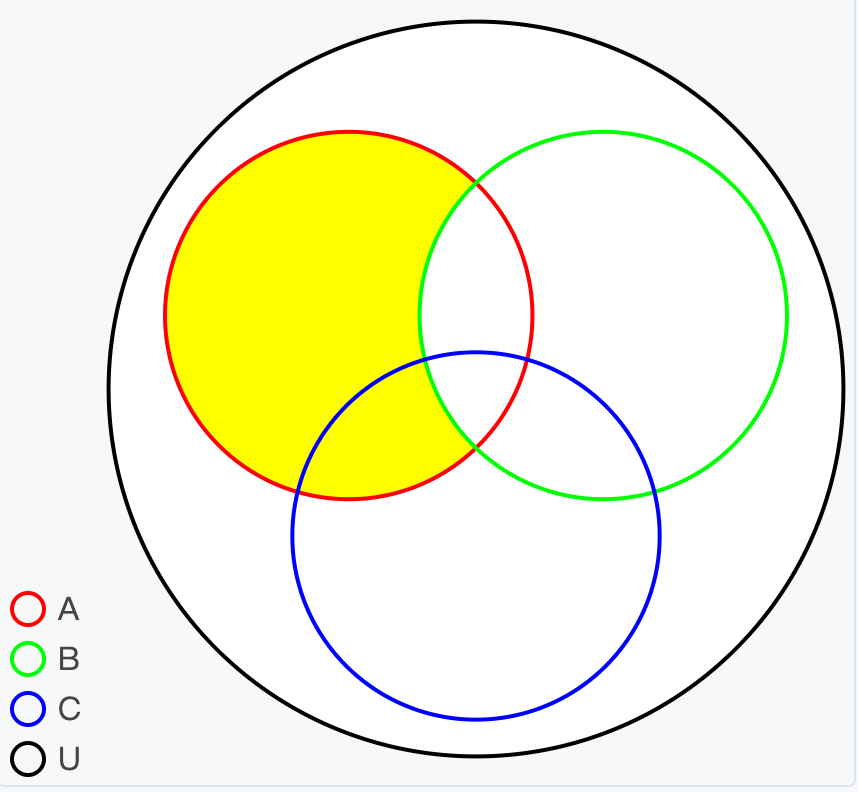
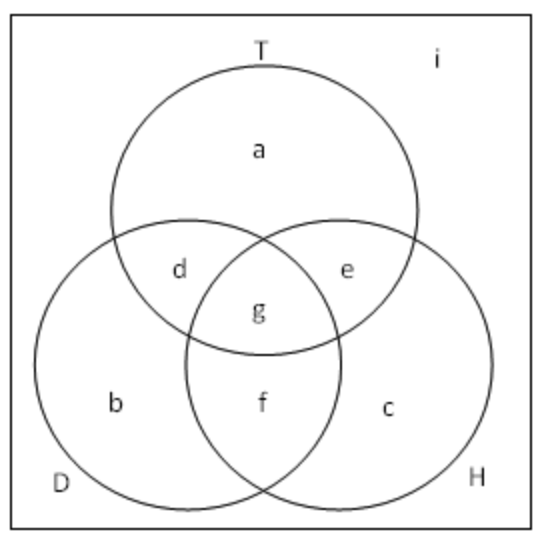
集合是具有某种特定性质的事物的全体,集合中的事物称为该集合的元素。维恩图是分析集合关系问题的图形化方法。
集合的基本概念
- 定义:用花括号表示的无序元素组
- 特点:
- 元素无序:
- 元素唯一:
- 表示方法:
符号表示
集合的表示法:
- 列举法:
- 描述法:
元素与集合的关系:
- :表示 是集合 的元素
- :表示 不是集合 的元素
集合间的关系:
- : 是 的子集
- : 是 的真子集
- : 和 相等
集合运算
运算 符号 含义 示例 并集 至少在一个集合中 交集 同时在两个集合中 补集 不在该集合中的元素 相对补 在A不在B中的元素 对称差 只在其中一个集合中
重要定理
- 子集定理:若 且 ,则
- 幂集定理:若集合 有 个元素,则其幂集 有 个元素
- 德摩根定律:
- 容斥原理:
例题1:集合等价性
问题:判断以下集合是否等价:
解答:和等价,因为包含相同元素
例题2:代数集合
若,求的值
解答:
- (验证不符合)
例题3:德摩根律应用
求
解答:使用德摩根律
- 由德摩根律,
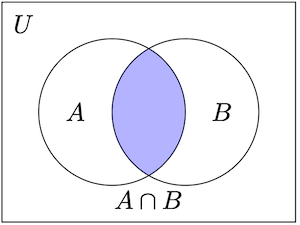
U
集合的全集