🎯 测验目标
- 检验基本概念理解
- 巩固符号和表示方法
- 强化运算法则记忆
- 识别常见错误陷阱
📝 答题说明
- 每张卡片点击翻转查看答案
- 自评掌握程度:已掌握/不确定/未掌握
- 记录错误概念以便重点复习
💡 概念测验卡片
card
什么是集合?给出数学化定义。
关键点:
- 特定性质
- 元素明确
- 元素互异
集合是具有某种特定性质的事物的总体,其中的每个事物称为该集合的元素。
提示
关键点:
- 特定性质
- 元素明确
- 元素互异
card
集合{x | x² < 9, x ∈ ℕ}用列举法如何表示?
解析:
1. x² < 9 意味着 -3 < x < 3
2. x ∈ ℕ 限制为自然数
3. 因此只有1, 2满足条件
{1, 2}
提示
解析:
- x² < 9 意味着 -3 < x < 3
- x ∈ ℕ 限制为自然数
- 因此只有1, 2满足条件
card
A ⊂ B 与 A ⊆ B 的区别是什么?
例如:
- {1,2} ⊂ {1,2,3}(真子集)
- {1,2} ⊆ {1,2}(子集但不是真子集)
- A ⊂ B:A是B的真子集,A包含于B且A≠B
- A ⊆ B:A是B的子集,A包含于B,可以A=B
提示
例如:
- {1,2} ⊂ {1,2,3}(真子集)
- {1,2} ⊆ {1,2}(子集但不是真子集)
card
写出德摩根律的两个公式。
应用提示:
- 运算符号改变(∪变∩,∩变∪)
- 各集合都要取补
- (A ∪ B)’ = A’ ∩ B’
- (A ∩ B)’ = A’ ∪ B’
提示
应用提示:
- 运算符号改变(∪变∩,∩变∪)
- 各集合都要取补
card
空集∅的三个重要性质是什么?
注意:空集≠{∅}
- 空集是任何集合的子集
- 空集的幂集是{∅}
- 空集的补集是全集
提示
注意:空集≠{∅}
card
如果A={1,2,3}, B={2,3,4},求A△B。
解析:
1. A△B = (A-B)∪(B-A)
2. A-B = {1}
3. B-A = {4}
4. 所以A△B = {1,4}
A△B = {1,4}
提示
解析:
- A△B = (A-B)∪(B-A)
- A-B = {1}
- B-A = {4}
- 所以A△B = {1,4}
card
在文氏图中,如何表示A∩B’?
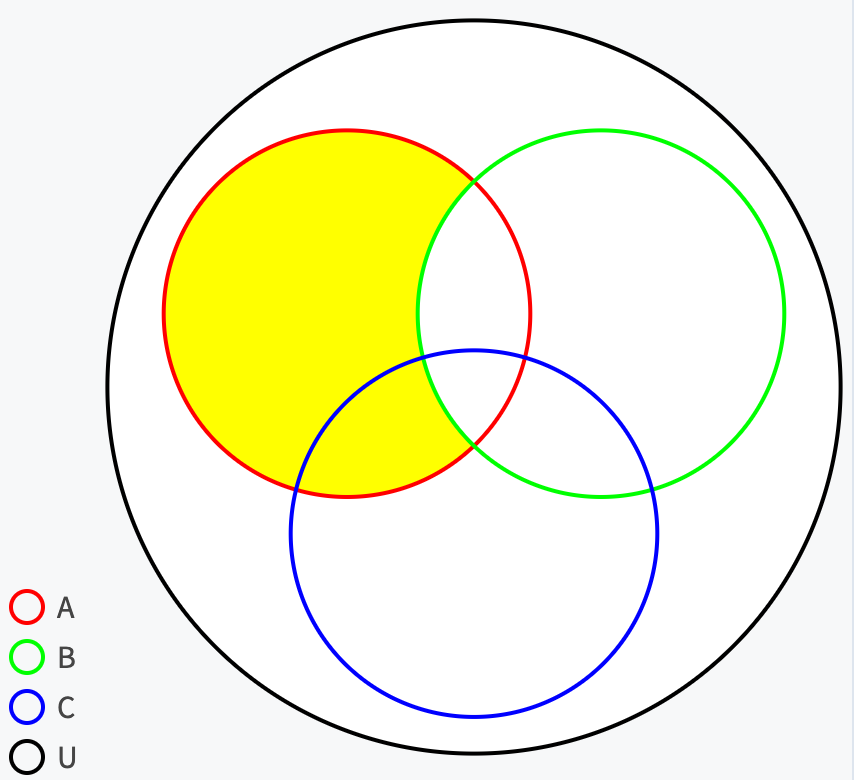
- 属于A但不属于B的区域
- 即A区域中排除A∩B的部分
提示
card
为什么说”所有学生的补集”这种表述是不严谨的?
这是集合论中常见的逻辑错误
- 补集必须相对全集而言
- 需要明确定义全集U
- 正确表述应为”在全体人类中,非学生的集合”
提示
这是集合论中常见的逻辑错误