三角函数
诱导公式
概念定义
三角函数诱导公式是描述特殊角度关系下三角函数值变化规律的公式集合。它建立了任意角与基本角之间的函数值对应关系,使我们能将任意角的三角函数值转化为第一象限内基本角的函数值。
主要类型包括:
- 周期性公式:基于函数周期性质,如
- 奇偶性公式:基于函数奇偶性,如
- 互补角公式:如
- 补角公式:如
- 转化公式:如
通俗理解
三角函数诱导公式就像数学的”角度变换器”,告诉我们如何在特殊角度间穿梭!当角度超出常规范围,或者变成负值、移动到其他象限时,三角函数值会怎样变化?诱导公式给出了明确答案!它让我们能把陌生角度”诱导”回熟悉区域,就像把外地人带到熟悉的地方一样。记住几个基本规律,我们就能算出任意角的三角函数值,角度再奇怪也不怕!
逻辑结构
逻辑结构
三角函数诱导公式形成一个完整的逻辑体系:
- 基础关系(起点):
(周期性)
(周期性)
(周期性)
(奇函数)
(偶函数)
(奇函数)
- 特殊角变换(核心):
- 象限规律(应用):
第一象限(0°~90°):所有三角函数值为正
第二象限(90°~180°):只有和为正
第三象限(180°~270°):只有和为正
第四象限(270°~360°):只有和为正
- 万能公式(整合):
- ,当为偶数时取"",为奇数时取""
- ,当为偶数时取"",为奇数时取""
图解思维
解决三角函数诱导公式问题的思维链:
- 分析角度类型 → 是否超出基本范围?在哪个象限?
- 确定转化策略 → 利用周期性减去或利用特殊角关系
- 提取基本角 → 找出第一象限内的对应角度
- 确定符号 → 根据象限位置或公式规则判断
- 计算最终值 → 基于基本角和符号调整
例如:求 思路: 利用周期性: 所以
应用示例
易错提醒
- 误区一:混淆不同函数的诱导公式(如搞错和的公式)
- 误区二:角度单位不统一(在计算中混用弧度和角度)
- 误区三:符号判断错误(特别是在第三、四象限)
- 边界情况:注意和在特定角度的无定义情况
- 常见错误:忽略周期对公式选择的影响
- 易错点:在诱导到基本角后,忘记根据原角度所在象限调整符号
最佳实践:熟记”奇变偶不变,符号看象限”,遇到复杂角度先化简为范围内的角
概念意义
三角函数诱导公式体现了数学思维中的”简化复杂”原则。它将无限多的角度情况,通过规律性的转换,归结为少量基本角的情况,展示了数学追求简洁统一的本质。
从认识论角度,诱导公式反映了人类思维寻找规律、建立联系的能力。它让我们看到看似不同的角度间存在着内在联系,体现了”纷繁多样中的统一规律”的哲学思想。
在实际应用中,诱导公式大大简化了三角计算,是解决周期性问题的基础工具。从天文学中的天体运动,到物理学中的波动现象,从工程学中的交流电路,到计算机图形学中的旋转变换,诱导公式都提供了高效处理角度变化的方法。
它培养了学生的”等价转换”思维,这种能力对数学乃至各种科学问题的解决都至关重要。掌握诱导公式,不仅是记住公式,更是理解周期性、对称性等数学核心概念的过程。
极简示例
问:计算的值。
解: 分析:位于第四象限,超出了基本角范围。
将其转化为基本角:
使用诱导公式:
再使用:
基本角
所以
或直接利用周期性和对称性:
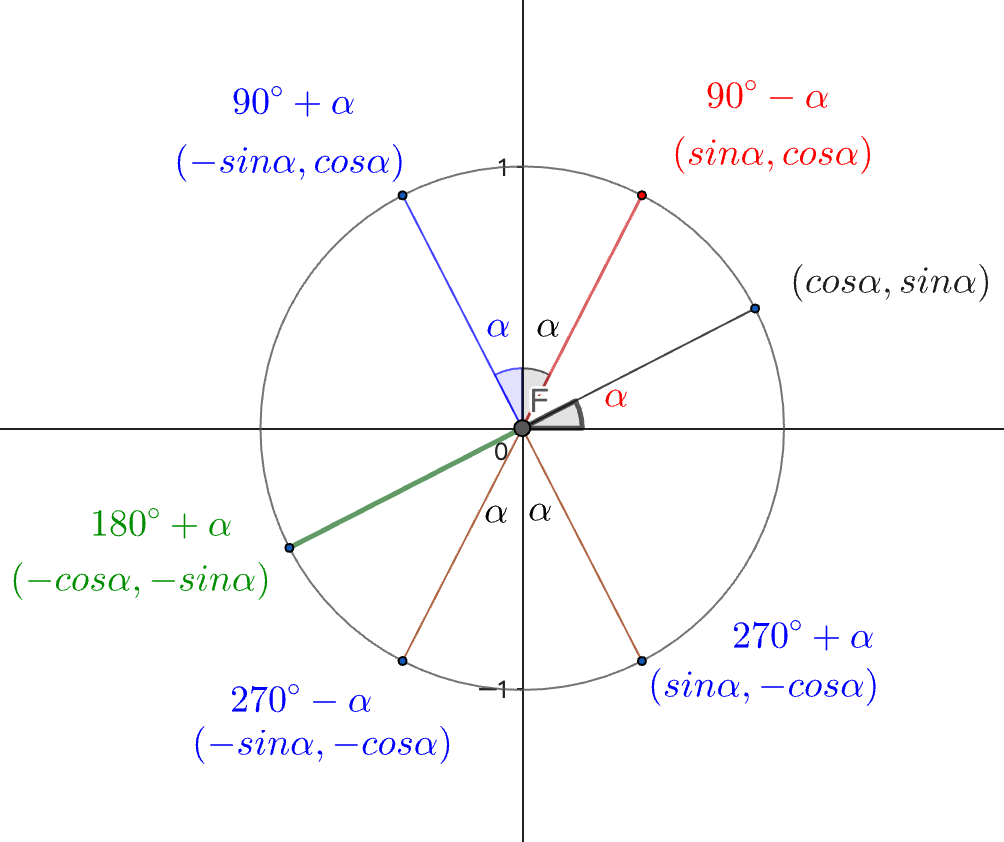
形象记忆
想象你带着一个三角函数计算器在单位圆上行走。诱导公式就像是一份”圆形地图导航”:
- 周期性:绕圆走一整圈,回到起点()
- 奇偶性:从原点出发,向相反方向走相同距离(角度变负)
- 象限变换:过了特殊点(、、),函数值有规律变化
记忆口诀:“奇变偶不变,符号看象限”——正弦余切是奇函数,负角会变负;余弦正割是偶函数,负角保持不变;至于符号,则要看角度落在哪个象限,遵循”正负负正”规律。
核心概念
- 基本角:第一象限内的锐角,通常指将任意角转化后的目标角
- 象限角:落在不同象限内的角
- 周期性:三角函数值随角度增加(或)而重复
- 奇偶性:函数关于原点或y轴的对称特性
- 商数关系:基本三角函数之间的比值关系
- 诱导公式:将任意角转化为基本角的规则系统
- 同角三角函数:同一角度下不同三角函数间的关系