概念定义
三角函数周期性是指三角函数的函数值按照一定角度间隔重复出现的性质。对于函数,若存在一个最小正数,使得对任意都有,则称为的周期。
基本三角函数的周期为:
- 正弦函数的周期是(或360°)
- 余弦函数的周期是(或360°)
- 正切函数的周期是(或180°)
- 余切函数的周期是(或180°)
- 正割函数的周期是(或360°)
- 余割函数的周期是(或360°)
通俗理解
三角函数就像大自然的循环节拍器!它们的值会像四季更替一样,固定地重复出现。正弦和余弦函数每转一圈(2π弧度或360度)就会完整重复一次,就像钟表的时针每12小时重复一次;而正切函数更”急性子”,只需半圈(π弧度或180度)就会重复,就像钟表的分针每30分钟就会回到相同的位置。这种有规律的重复,让我们能预测周期性变化的未来!
逻辑结构
三角函数周期性的逻辑体系:
- 基本周期关系:
- 推广公式:对任意整数
- 复合周期:
- 若周期为,周期为,则的周期为和的最小公倍数
- 函数的周期为
- 奇偶性与周期的关系:
- (奇函数)
- (偶函数)
- (奇函数)
图解思维
解决三角函数周期性问题的思维链:
- 识别函数类型 → 基本三角函数还是复合函数?
- 确定基本周期 → 正弦余弦是2π,正切余切是π
- 分析变形影响 → 振幅系数不影响周期,频率系数会改变周期
- 计算实际周期 → (ω是角频率)
- 处理复合函数 → 求各部分周期的最小公倍数
例如:函数的周期是多少? 周期为,周期为,最小公倍数为
易错提醒
- 误区一:认为所有三角函数周期都是(错!正切和余切函数周期是)
- 误区二:忽略系数对周期的影响(错!的周期是)
- 误区三:混淆振幅与周期(错!中只影响振幅,不影响周期)
- 边界情况:是常数函数,不具有周期性;而在处没有定义
- 易错点:求复合函数周期时,简单相加而不求最小公倍数
概念意义
三角函数周期性体现了自然界中普遍存在的循环规律。从哲学层面看,它展示了”变中有不变”的辩证思想——函数值不断变化,但变化模式却始终如一。这种周期性为我们提供了描述和预测各种循环现象的数学工具。
在物理学中,三角函数周期性是描述波动、振动、电磁场等现象的基础;在信号处理中,它是傅里叶分析的核心;在音乐中,它解释了和声的数学本质;在工程中,它帮助分析结构振动和交流电路。
三角函数周期性的发现,让人类能够用简洁的数学语言捕捉自然界中看似复杂的周期变化,是人类认识规律、应用规律的智慧结晶。
极简示例
问:函数的周期是多少?
解: 的周期为 的周期为
求最小公倍数:
和的最小公倍数是,所以的周期是。
验证:
核心概念
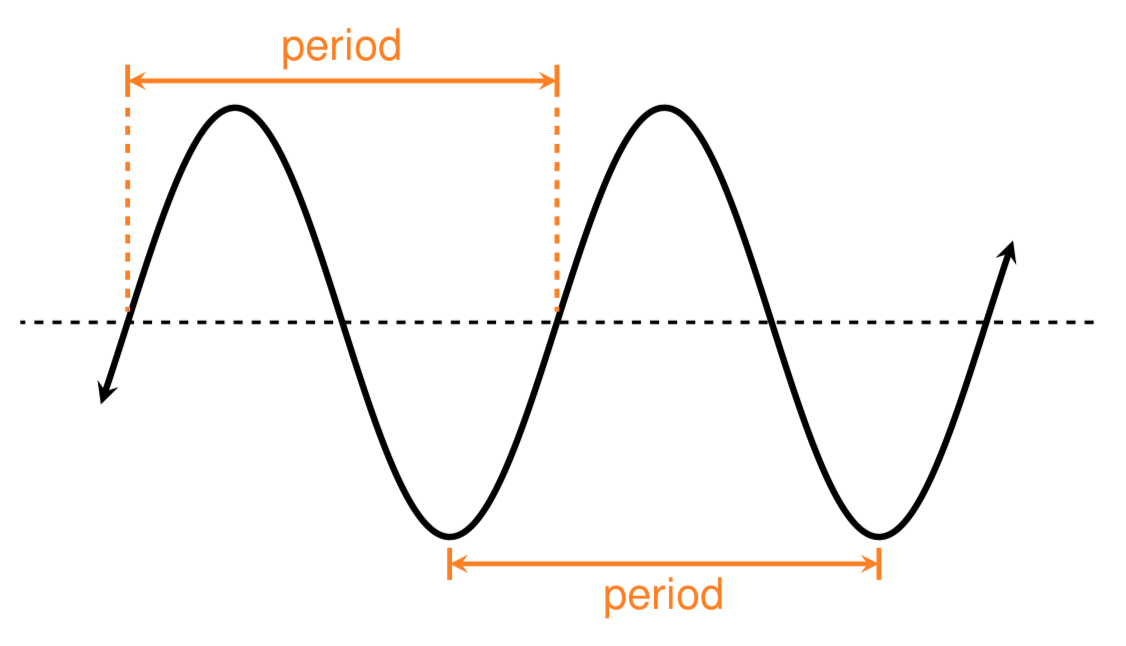
- 周期:函数完成一次完整变化所需的自变量变化量
- 最小正周期:使函数值重复的最小正数变化量
- 函数值域:函数输出的全部可能值范围
- 振幅:周期函数波动的幅度(最大值与最小值之差的一半)
- 相位:描述周期函数在周期内的位置
- 频率:单位时间/角度内完成周期的次数(周期的倒数)