三角函数对称性

三角函数的对称性研究函数关于y轴、原点的对称特征，以及周期性质中的角度对称关系。

基本对称性质

函数函数性质对称性质数学表达式
正弦奇函数原点对称 $sin (- θ) = - sin (θ)$
余弦偶函数 y轴对称 $cos (- θ) = cos (θ)$
正切奇函数原点对称 $tan (- θ) = - tan (θ)$

函数	函数性质	对称性质	数学表达式
正弦	奇函数	原点对称	$sin (- θ) = - sin (θ)$
余弦	偶函数	y轴对称	$cos (- θ) = cos (θ)$
正切	奇函数	原点对称	$tan (- θ) = - tan (θ)$

card

基本对称性

关于y轴的对称性

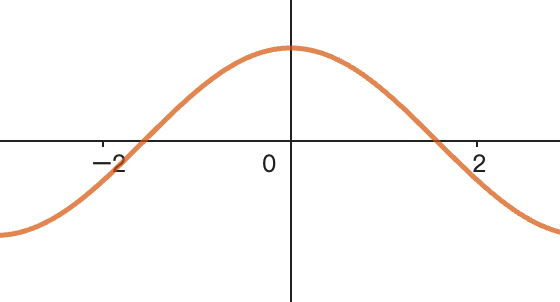
![](https://xdwise-1253986005.cos.ap-nanjing.myqcloud.com/202501151315733.png)

$cos (- x) = cos (x)$ # 偶函数

more_vert

提示

card

基本对称性

关于原点的对称性

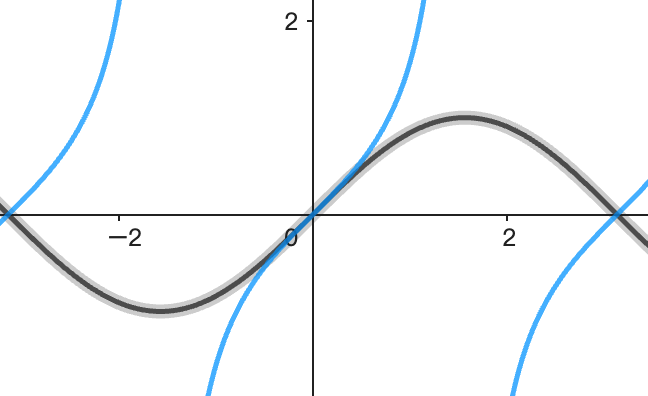
![](https://xdwise-1253986005.cos.ap-nanjing.myqcloud.com/202501151952694.png)

$s in (x + π) = - s in (x)$ $t an (x + π) = t an (x)$ # 周期性

more_vert

提示

card

2. 特殊角度对称

1. 关于90°(π/2)对称

sin(90°+α): “sin(90°-α)”

cos(90°+α): “-cos(90°-α)”

tan(90°+α): “-cot(α)”

2. 关于180°(π)对称

sin(180°+α): -sin(α)

cos(180°+α): -cos(α)

tan(180°+α): tan(α)

3. 关于270°(3π/2)对称

sin(270°+α): -sin(270°-α)

cos(270°+α): cos(270°-α)

tan(270°+α): -cot(α)

more_vert

card

3. 象限对称性

第一象限： > $s in α = cos (9 0^{\circ} - α)$ > $cos α = s in (9 0^{\circ} - α)$ 第二象限: sin(180°-α): “sin(α)” cos(180°-α): “-cos(α)” tan(180°-α): “-tan(α)” 第三象限: sin(180°+α): “-sin(α)” . > cos(180°+α): “-cos(α)” tan(180°+α): “tan(α)” 第四象限: sin(360°-α): “-sin(α)” cos(360°-α): “cos(α)” tan(360°-α): “-tan(α)”

more_vert

函数对称类型

偶函数特征：

$f (- x) = f (x)$

关于y轴对称

例： $cos x$ , $sec x$

奇函数特征：

$f (- x) = - f (x)$

关于原点对称

必过原点

例： $sin x$ , $tan x$

角度对称关系

sin(90°+α): “sin(90°-α)” cos(90°+α): “-cos(90°-α)” tan(90°+α): “-cot(α)“

角度关系正弦余弦正切
$θ + π$ $- sin θ$ $- cos θ$ $tan θ$
$- θ$ $- sin θ$ $cos θ$ $- tan θ$
$π - θ$ $sin θ$ $- cos θ$ $- tan θ$

角度关系	正弦	余弦	正切
$θ + π$	$- sin θ$	$- cos θ$	$tan θ$
$- θ$	$- sin θ$	$cos θ$	$- tan θ$
$π - θ$	$sin θ$	$- cos θ$	$- tan θ$

复合函数对称性

两个偶函数的和是偶函数

两个奇函数的积是偶函数

奇函数与偶函数的积是奇函数

判断步骤：

代入 $- x$

利用基本对称性质

比较 $f (- x)$ 和 $f (x)$ 或 $- f (x)$

4. 应用要点

化简计算

calculation_tips:
  - "利用对称性将角度化到第一象限"
  - "利用特殊角对称简化计算"
  - "利用周期性处理大角度"

方程求解

equation_solving:
  - "利用对称性找到所有解"
  - "注意解的范围限制"
  - "考虑周期性解"

图像分析

graph_analysis:
  - "利用对称性快速描点"
  - "判断函数奇偶性"
  - "确定图像对称轴"

5. 记忆方法

规律总结

memory_rules:
  - "正弦在第二象限同名同号"
  - "余弦在第四象限同名同号"
  - "正切在第一三象限同名同号"

口诀记忆

memory_tips:
  - "奇变偶不变，符号看象限"
  - "正弦余弦和正切，一二三四象限中"
  - "象限角的符号判断：All Science Teachers Care"

6. 常见错误

common_mistakes:
  - "忽略角度范围限制"
  - "符号判断错误"
  - "对称轴选择错误"
  - "周期性使用不当"

7. 练习建议

practice_suggestions:
  basic:
    - "从第一象限开始，逐步扩展"
    - "特殊角度重点练习"
    - "对称性规律总结"
  
  advanced:
    - "综合运用多种对称性"
    - "解决复杂角度问题"
    - "图像性质分析"

需要我详细展开某个方面吗？