投影🔎

概念定义

在三角函数中，投影指的是一个线段或向量在特定方向上的映射长度。

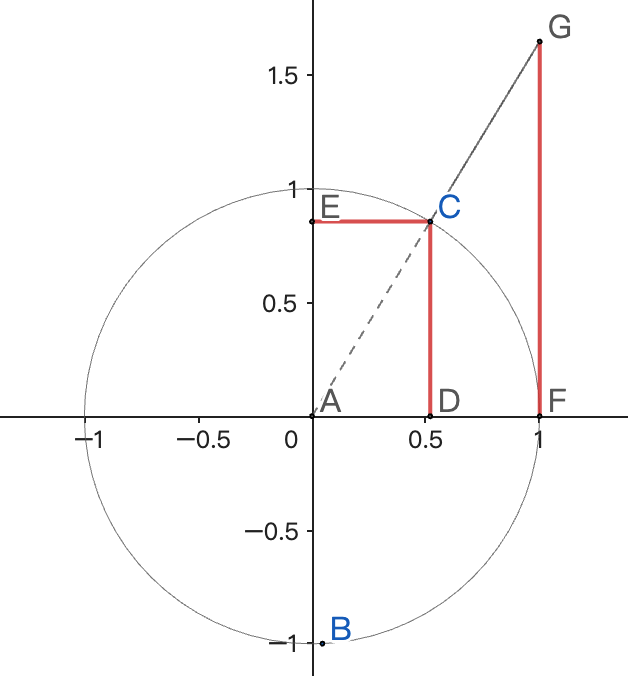
对于单位圆上角度为θ的点P(cosθ, sinθ)：

• 正弦函数sinθ表示点P在y轴上的投影值
• 余弦函数cosθ表示点P在x轴上的投影值
• 正切函数tanθ表示从原点到点P的射线在x=1处的y值（垂直投影高度）

投影长度的符号: 取决于投影方向与坐标轴正方向的关系，具有正负性。

核心概念

• 投影：几何体在特定方向上的”影子”长度
• 单位圆：半径为1的圆，是理解三角函数的几何模型
• 坐标投影：点在坐标轴上的投影值，即点的坐标分量
• 正交分解：将向量分解为互相垂直的两个分量
• 投影符号：根据投影方向与坐标轴正方向的关系确定
• 周期变化：投影长度随角度变化呈现周期性规律
• 相位差：不同投影方向的周期变化之间的角度差异

逻辑结构

三角函数投影概念形成一个完整的逻辑体系：

1. 基础定义（几何意义）：

• 单位圆上点P到x轴的垂直距离 = sinθ

• 单位圆上点P到y轴的垂直距离 = cosθ

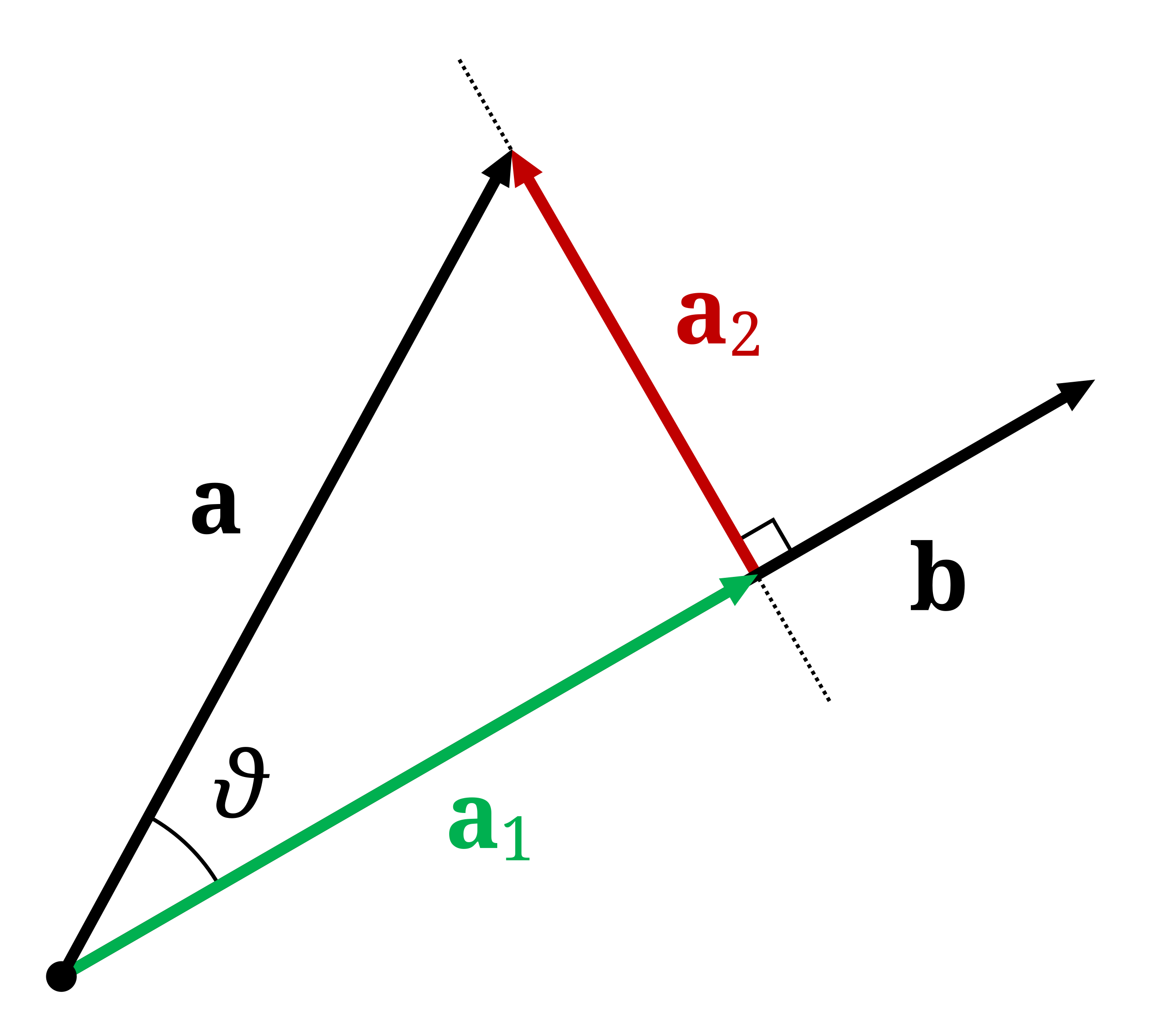
1. 向量与投影：

• 向量在x轴上的投影 = |向量|·cosθ

• 向量在y轴上的投影 = |向量|·sinθ

• 向量在任意方向上的投影 = |向量|·cos(α)（α为向量与投影方向的夹角）

3. 投影关系（三角恒等式）：

• 投影平方和：sin²θ + cos²θ = 1

• 互补角关系：sin(90°-θ) = cosθ，cos(90°-θ) = sinθ（垂直方向的投影关系）

• 负角关系：sin(-θ) = -sinθ，cos(-θ) = cosθ（投影的对称性）

4. 投影变化（函数特性）：

• 正弦投影：从0开始，先增加后减
• 余弦投影：从1开始，先减小后增加
• 正切投影：表示斜率