$f(x) = \arccos(2x^2-1)$

设函数 $f(x)=\arccos (2x^2-1)$，求函数 $f(x)$ 的定义域和值域，并分析其单调性。̂

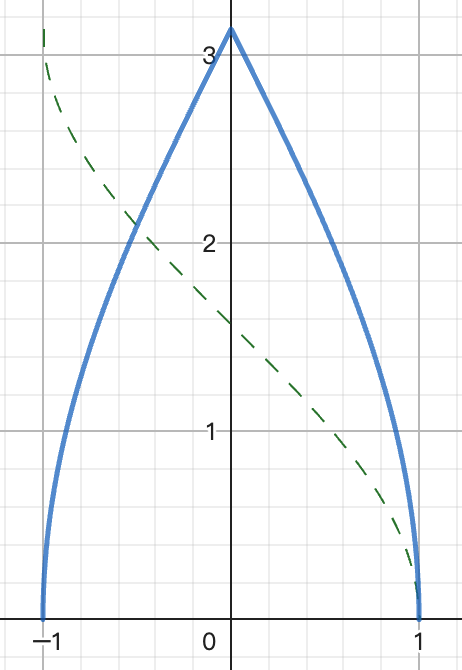
步骤1：确定定义域 反余弦函数 $\arccos (t)$ 的定义域是 $[-1,1]$，所以需要满足： $-1\le 2x^2-1\le 1$

解不等式： $-1\le 2x^2-1\le 1$ $0\le 2x^2\le 2$ $0\le x^2\le 1$ $0\le |x|\le 1$ $-1\le x\le 1$

因此，函数 $f(x)=\arccos (2x^2-1)$ 的定义域是 $[-1,1]$。

步骤2：确定值域 当 $x\in [-1,1]$ 时，$x^2\in [0,1]$，所以 $2x^2-1\in [-1,1]$ 当 $x=0$ 时，$2x^2-1=-1$，此时 $f(0)=\arccos (-1)=\pi$ 当 $x=\pm 1$ 时，$2x^2-1=1$，此时 $f(\pm 1)=\arccos (1)=0$

由于 $\arccos (t)$ 在 $[-1,1]$ 上是单调递减函数，当 $t$ 从 $-1$ 增加到 $1$ 时，$\arccos (t)$ 从 $\pi$ 减少到 $0$。 因此，函数 $f(x)=\arccos (2x^2-1)$ 的值域是 $[0,\pi ]$。

步骤3：分析单调性 令 $g(x)=2x^2-1$，则 $f(x)=\arccos (g(x))$

$g^{\prime }(x)=4x$，当 $x>0$ 时，$g^{\prime }(x)>0$，$g(x)$ 单调递增； 当 $x<0$ 时，$g^{\prime }(x)<0$，$g(x)$ 单调递减。

由于 $\arccos (t)$ 是单调递减函数，所以：

• 当 $x>0$ 时，$g(x)$ 单调递增，$f(x)$ 单调递减
• 当 $x<0$ 时，$g(x)$ 单调递减，$f(x)$ 单调递增

因此，$f(x)$ 在区间 $[-1,0]$ 上单调递增，在区间 $[0,1]$ 上单调递减，$x=0$ 是函数的极大值点。

• 反余弦函数 (Arccos)>>