从外心的视角解释正弦

传统定义

在直角三角形中，正弦定义为对边与斜边的比值： $\sin \alpha =\frac{对边}{斜边}$

外心视角定义

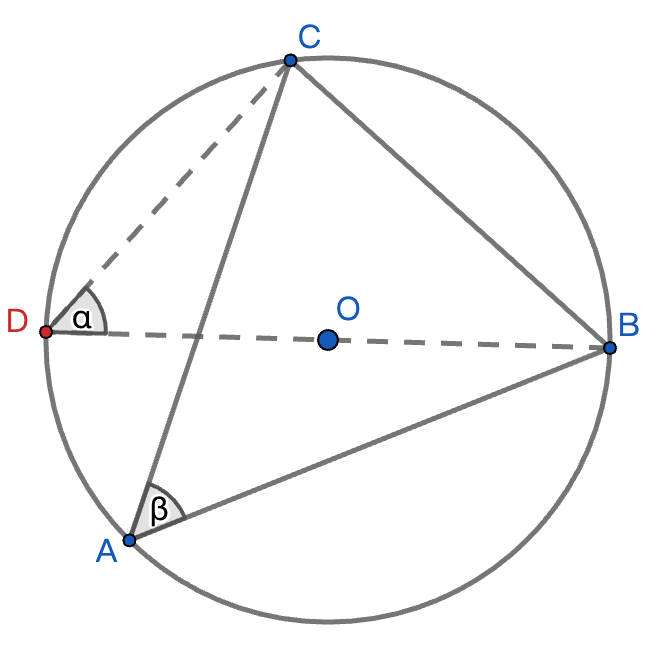
1. 基于外接圆的定义
   1. ==对任意角$\alpha$，其正弦值等于以外心为圆心、半径为R的圆上，该角所对的弦长的一半除以半径==
   2. $\sin \alpha =\frac{弦长}{2R}$
2. 几何解释
   1. 在半径为R的圆中，角$\alpha$对应的弦长为$2R\sin \alpha$
   2. 这说明正弦实际上是在单位圆（R=1）中，角所对应的弦长的一半

1. 统一性

   1. 这个定义对任意角度都适用
   2. 不局限于直角三角形
   3. 自然引出了正弦的周期性

2. 几何意义

   1. 正弦值反映了角在圆周上张角对应的弦长与半径的比值关系
   2. 体现了角度和长度的统一
   3. 解释了为什么$|\sin \alpha |\le 1$

1. 直接推论 - 在三角形ABC中，边$a=2R\sin A$ - 这直接导出了$\frac{a}{\sin A}=2R$ - 解释了为什么正弦定理中出现2R这个量

2. 统一解释 - 三角形的每条边都是其外接圆上的弦 - 每个角所对的弦长都是$2R\sin$值 - 这解释了为什么边与正弦值成比例