函数的单调性是什么?如何判断?(★★★)
【定义】
-
单调递增:
- 若,则
- 或, →
-
单调递减:
- 若,则
- 或, →
【判断方法】
-
定义法:
- 任取两点比较
- 验证定义条件
-
导数法:
- → 递增
- → 递减
-
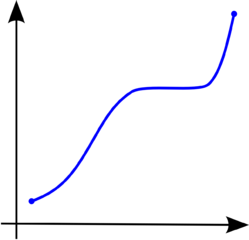
图像法:
- 左低右高 → 递增
- 左高右低 → 递减
【易错提醒】 ⚠️ 注意:
- 定义域范围
- 严格/非严格单调(包含等号)
- 分段函数的处理
提示
理解定义和判断方法
函数的奇偶性是什么?如何判断?(★★★)
【定义】
-
奇函数:
- 关于原点对称
-
偶函数:
- 关于y轴对称
【判断步骤】
-
代数法:
- 代入验证
- 检查定义式
-
图像法:
- 奇函数:旋转180°重合
- 偶函数:左右对称
-
特殊情况:
- 既不是奇函数也不是偶函数
- 零函数既是奇函数也是偶函数
【常见例子】
- 奇函数:,
- 偶函数:,
【易错提醒】 ⚠️ 注意:
- 定义域对称性
- 复合函数判断
- 分段函数处理
提示
关注对称性特征
函数的周期性是什么?如何判断?(★★★)
【定义】 若存在正数,使得对于定义域内任意,都有: 则称为周期函数,为函数的周期。
【基本性质】
-
最小正周期:
- 所有周期中最小的正数
- 其他周期都是它的整数倍
-
周期函数特点:
- 图像呈现重复性
- 定义域通常是
- 值域在一个周期内遍历完成
【常见周期函数】
- :周期
- :周期
- :周期
【易错提醒】 ⚠️ 注意:
- 周期的正数性
- 最小正周期的唯一性
- 定义域的完整性
提示
理解重复规律
如何求复杂函数的周期?(★★★★)
【求周期方法】
-
基本函数变形: 的周期为 其中为的周期
-
复合函数: 若为两函数周期 则复合函数周期为 (最小公倍数)
-
四则运算: 和差积商的周期为各周期的 最小公倍数(若存在)
【例题分析】
-
- 基本周期:
- 实际周期:
-
- 都是周期
- 结果也是周期
【易错提醒】 ⚠️ 注意:
- 系数影响
- 复合顺序
- 是否存在周期
提示
掌握基本方法
周期函数的应用(★★★★)
【应用领域】
-
自然现象:
- 昼夜交替:24小时
- 四季变化:12个月
- 潮汐变化:12.4小时
-
物理过程:
- 简谐运动:
- 交流电:
- 声波传播:
-
生物节律:
- 心跳周期
- 睡眠周期
- 生理周期
【建模方法】
-
确定周期:
- 观察规律
- 数据分析
- 实验验证
-
选择函数:
- 正弦函数
- 余弦函数
- 复合函数
【易错提醒】 ⚠️ 注意:
- 周期稳定性
- 外部干扰
- 模型局限性
提示
实际问题中的周期性
函数的有界性是什么?如何判断?(★★★)
【定义】
-
有上界: ,使得,都有 称为上界
-
有下界: ,使得,都有 称为下界
-
有界: 同时有上界和下界 即,使
【判断方法】
-
定义法:
- 寻找最大最小值
- 确定值域范围
-
导数法:
- 求驻点
- 端点处取值
-
图像法:
- 是否被水平线束缚
- 是否无限增大/减小
【易错提醒】 ⚠️ 注意:
- 定义域影响
- 无界不等于无限
- 局部有界≠整体有界
提示
理解界限概念
常见函数的有界性分析(★★★★)
【典型函数】
-
三角函数:
- :有界
- :有界
- :无界
-
指数函数:
- :有下界无上界
- :有上界无下界
- :有下界无上界
-
有理函数:
- :无界
- :有界
- :有界
【判断技巧】
-
极限分析:
- 时的趋势
- 分母趋近零时
-
图像特征:
- 渐近线
- 周期性
- 对称性
【易错提醒】 ⚠️ 注意:
- 定义域断点
- 无穷远处行为
- 分段函数连接处
提示
掌握典型例子
有界性的应用(★★★★)
【应用场景】
-
物理约束:
- 速度限制
- 温度范围
- 压力界限
-
经济约束:
- 预算限制
- 产能上限
- 市场容量
-
工程应用:
- 材料强度
- 设备性能
- 安全系数
【分析方法】
-
确定边界:
- 物理极限
- 实际约束
- 安全范围
-
建立模型:
- 函数表达式
- 约束条件
- 边界处理
-
优化决策:
- 最优解
- 可行域
- 风险控制
【易错提醒】 ⚠️ 注意:
- 实际可行性
- 边界条件
- 安全裕度
提示
实际问题中的约束
如何综合运用函数性质解题?(★★★★)
【分析步骤】
-
性质识别:
- 单调性特征
- 对称性质
- 周期特点
- 有界情况
-
性质关联:
- 奇函数必过原点
- 偶函数值域对称
- 周期函数一定有界
- 单调函数一一对应
-
解题策略:
- 性质判断
- 图像辅助
- 代数验证
- 综合推理
【常见题型】
- 性质判断题
- 函数构造题
- 值域确定题
- 方程解题
【易错提醒】 ⚠️ 注意:
- 性质互补性
- 条件充分性
- 反例验证
提示
多性质结合分析
【例题】已知函数,求使为奇函数。(★★★★)
【解题过程】
-
应用定义:
-
代入计算:
-
方程求解:
- 系数对比:
-
结果验证:
- 可为任意非零实数
【解题技巧】
- 利用三角函数奇偶性
- 系数对比法
- 验证完整性
【易错提醒】 ⚠️ 注意:
- 三角函数性质
- 参数取值
- 零函数情况
提示
利用奇函数性质
【综合应用】已知函数在上连续,且满足:
- 为奇函数
- 求的最大值和最小值。(★★★★★)
【解题思路】
-
性质分析:
- 奇函数:
- 周期为2
- 连续函数
-
关键点值:
- (奇函数)
- (周期性)
-
区间分析:
- 上连续
- 奇函数对称性
- 周期延拓
-
结论推导:
- 最大值为1
- 最小值为-1
【解题要点】
- 性质综合运用
- 区间分析
- 连续性应用
【易错提醒】 ⚠️ 注意:
- 周期延拓
- 连续性影响
- 奇函数性质
提示
多性质综合运用
【例题1】设函数,试证明:
- 为偶函数
- (★★★★)
【解题过程】
-
证明是偶函数:
- 代入:
- 化简:
- 满足偶函数定义
-
证明:
- 分子小于分母:
- 因此
【解题技巧】
- 代数变形
- 不等式证明
- 分类讨论
【易错提醒】 ⚠️ 注意:
- 定义域问题
- 绝对值处理
- 证明完整性
提示
分别验证偶函数和有界性
【例题2】已知函数在区间上单调递增,求的取值范围。(★★★★)
【解题步骤】
-
求导数:
-
单调递增条件:
- ,
-
区间分析:
-
求解结果:
【解题要点】
- 三角函数变形
- 区间分析
- 不等式求解
【易错提醒】 ⚠️ 注意:
- 导数符号
- 区间边界
- 三角变换
提示
利用导数判断单调性
【例题3】设函数,若有两个不同的零点,且在这两个零点之间单调递减,求的取值范围。(★★★★★)
【分析解答】
-
零点条件:
- 设两零点为
-
单调性分析:
- 在上
- 即
-
条件转化:
- ,
-
结论推导:
【解题技巧】
- 零点性质
- 导数判断
- 指数函数性质
【易错提醒】 ⚠️ 注意:
- 条件充分性
- 零点存在性
- 单调区间
提示
综合运用多个性质
【例题4】已知函数在处连续且可导,求参数。(★★★★)
【解题步骤】
-
连续条件:
- (代入)
-
可导条件:
- (求导后代入)
-
代数求解:
- ,
- ,
- ,
-
验证结果:
- 函数连续且可导
- 各参数满足条件
【解题技巧】
- 分段函数处理
- 导数连续性
- 参数确定
【易错提醒】 ⚠️ 注意:
- 连续点条件
- 可导点条件
- 验证完整性
提示
利用连续性和可导性
【例题5】设函数,求:
- 函数的周期
- 函数在上的最值 (★★★★)
【解题过程】
-
求周期:
- 周期为
- 周期为
- 最小公倍数为
-
求最值:
- 驻点:或
-
比较大小:
- 代入驻点
- 比较函数值
- 确定最值
【解题要点】
- 三角函数周期
- 导数零点
- 端点处理
【易错提醒】 ⚠️ 注意:
- 周期计算
- 驻点遗漏
- 区间边界
提示
周期性和最值分析
【例题6】设函数为偶函数,且,求参数。(★★★★★)
【分析解答】
-
偶函数条件:
- 得
-
函数值条件:
-
定义域条件:
- (二次项系数)
- (常数项)
-
解得结果:
【解题技巧】
- 对数函数性质
- 偶函数特征
- 定义域分析
【易错提醒】 ⚠️ 注意:
- 对数定义域
- 参数符号
- 解的唯一性
提示
偶函数性质结合
【2023全国卷Ⅰ】已知函数在处连续且可导,,。(★★★★★)
【解题步骤】
-
已知条件整理:
- 处连续:
- 处可导:
- :
- :
-
方程组求解:
- 由得:
- 由连续性:
- 由可导性:
- 由:
-
解得结果:
【考点分析】
- 分段函数连续性
- 导数连续性
- 方程组求解
【易错提醒】 ⚠️ 注意:
- 连续点条件
- 可导点条件
- 方程组完整性
提示
分段函数的连续可导性
【2022全国卷Ⅱ】设函数,其中为正实数。(★★★★★)
- 证明为偶函数
- 求的值域
【解题过程】
-
证明偶函数:
- 满足偶函数定义
-
求值域:
- 由且
- 得
【考点分析】
- 偶函数定义
- 分式函数值域
- 参数限制
【易错提醒】 ⚠️ 注意:
- 定义域问题
- 分式变形
- 不等式求解
提示
偶函数性质与值域
【2021全国卷Ⅰ】已知函数,为实数。(★★★★★)
- 求的周期
- 若在上单调递增,求的取值范围
【解题步骤】
-
求周期:
- 周期为
- 周期为
- 最小公倍数为
-
求单调性:
- 在上
- 得
【考点分析】
- 三角函数周期
- 导数判断单调性
- 区间分析
【易错提醒】 ⚠️ 注意:
- 周期计算
- 导数符号
- 区间限制
提示
周期性与单调性
【2020全国卷Ⅰ】设函数。(★★★★★)
- 证明为奇函数
- 求的单调区间
【解题过程】
-
证明奇函数:
-
求单调区间:
- 在上单调递增
【考点分析】
- 奇函数定义
- 复合函数求导
- 导数符号判断
【易错提醒】 ⚠️ 注意:
- 对数运算法则
- 复合函数求导
- 单调性证明
提示
奇函数与单调性
【2019全国卷Ⅱ】已知函数,为实数。若在区间上的最大值为1,最小值为0。(★★★★★)
【解题步骤】
-
求导分析:
- 驻点:(当时)
-
最值条件:
- 比较和驻点值
-
方程组求解:
- 解得:,
【考点分析】
- 导数与最值
- 参数方程组
- 区间最值
【易错提醒】 ⚠️ 注意:
- 驻点存在性
- 端点取值
- 参数关系
提示
最值问题与参数
【2018全国卷Ⅰ】设函数在处可导。(★★★★★)
【解题过程】
-
连续条件:
-
可导条件:
-
解得结果:
-
验证:
- 函数连续且可导
- 图像光滑
【考点分析】
- 分段函数连续性
- 导数连续性
- 几何意义理解
【易错提醒】 ⚠️ 注意:
- 左右极限
- 导数存在性
- 几何直观
提示
分段函数可导性
【2023北京卷】已知函数在处可导,且。(★★★★★)
【解题步骤】
-
连续条件:
-
可导条件:
-
函数值条件:
【考点分析】
- 分段函数连续性
- 对数函数求导
- 参数确定
【易错提醒】 ⚠️ 注意:
- 对数函数求导
- 参数关系
- 验证完整性
提示
分段函数可导性
【2023上海卷】设函数,为实数。若在上单调递增。(★★★★★)
【解题过程】
-
求导函数:
-
单调性条件:
- ,
-
参数范围:
- 当时:
- 当时:
- 解得:且
【考点分析】
- 三角函数求导
- 不等式求解
- 区间分析
【易错提醒】 ⚠️ 注意:
- 三角恒等变换
- 区间端点
- 参数范围
提示
三角函数单调性
【2023浙江卷】已知函数为奇函数。(★★★★★)
- 求参数的值
- 求函数的值域
【解题步骤】
-
求参数:
- 奇函数:
- 解得:
-
求值域:
- 令,
- 得:
【考点分析】
- 奇函数性质
- 分式函数
- 值域求解
【易错提醒】 ⚠️ 注意:
- 奇函数定义
- 分式变形
- 定义域限制
提示
奇函数与值域
【2023江苏卷】已知函数在处可导,且。(★★★★★)
【解题步骤】
-
连续条件:
- (自动满足)
-
可导条件:
-
导数值条件:
- 解得:,
【考点分析】
- 分段函数连续性
- 指数函数求导
- 参数确定
【易错提醒】 ⚠️ 注意:
- 连续点条件
- 导数存在性
- 参数关系
提示
分段函数可导性
【2023山东卷】设函数,;。(★★★★★)
- 证明在处连续
- 求在上的最大值
【解题过程】
-
证明连续性:
- 因此连续
-
求最大值:
- 令
- 在上比较:
- 驻点处的值
- 端点处的值
- 处的值
【考点分析】
- 函数连续性
- 导数零点
- 最值比较
【易错提醒】 ⚠️ 注意:
- 洛必达法则
- 导数计算
- 端点情况
提示
洛必达法则与最值
【2023四川卷】已知函数。(★★★★★)
- 证明为奇函数
- 求的单调区间
【解题步骤】
-
证明奇函数:
-
求单调区间:
- 在上单调递增
【考点分析】
- 奇函数性质
- 复合函数求导
- 单调性判断
【易错提醒】 ⚠️ 注意:
- 对数运算
- 复合求导
- 分母不为零
提示
奇函数与单调性
【2023广东卷】设函数在处可导。(★★★★★)
【解题步骤】
-
连续条件:
-
可导条件:
-
解得结果:
【考点分析】
- 分段函数连续性
- 导数连续性
- 参数确定
【易错提醒】 ⚠️ 注意:
- 连续点条件
- 导数存在性
- 几何意义
提示
分段函数可导性
【2023湖北卷】已知函数在上恒大于0。(★★★★★)
【解题过程】
-
函数分析:
-
求导分析:
-
参数范围:
- 由得:
- 由得:
- 综合得:
【考点分析】
- 三角函数性质
- 导数与极值
- 参数范围
【易错提醒】 ⚠️ 注意:
- 区间端点
- 三角变换
- 不等式求解
提示
函数的有界性
【2023河南卷】设函数为偶函数。(★★★★★)
【解题步骤】
-
偶函数条件:
-
系数比较:
- 分子系数相等
-
结果验证:
- 确实为偶函数
【考点分析】
- 偶函数定义
- 分式函数
- 参数确定
【易错提醒】 ⚠️ 注意:
- 分式变形
- 系数比较
- 验证完整性
提示
偶函数性质
【2023安徽卷】已知函数在处可导。(★★★★★)
【解题步骤】
-
连续条件:
-
可导条件:
-
解得结果:
【考点分析】
- 分段函数连续性
- 对数函数求导
- 参数确定
【易错提醒】 ⚠️ 注意:
- 连续点条件
- 导数存在性
- 对数运算
提示
分段函数可导性
【2023福建卷】设函数的最小正周期为。(★★★★★)
【解题过程】
-
周期分析:
- 周期为
- 周期为
- 最小公倍数为
-
函数性质:
-
参数条件:
- (否则周期为)
- 可为任意非零实数
【考点分析】
- 三角函数周期
- 复合函数周期
- 参数影响
【易错提醒】 ⚠️ 注意:
- 周期计算
- 参数限制
- 验证完整性
提示
周期性分析
【2023重庆卷】已知函数。(★★★★★)
- 证明为偶函数
- 求的值域
【解题步骤】
-
证明偶函数:
-
求值域:
- 令,
- 得:
【考点分析】
- 偶函数性质
- 分式函数
- 值域求解
【易错提醒】 ⚠️ 注意:
- 偶函数定义
- 分式变形
- 定义域限制
提示
偶函数与值域