什么是指数函数?其基本形式是什么?(★★)
【核心结论】 指数函数的一般形式: (其中且)
- 称为底数
- 是指数,为自变量
【记忆技巧】 想象”细胞分裂”:
- 如果:一个细胞不断翻倍()
- 如果:一个整体不断对半分
【重要特点】
- 定义域:
- 值域:
- 过点
【易错警示】 ⚠️ 注意:
- 底数必须大于0
- 时退化为常数函数
提示
观察y=2^x的形式特点
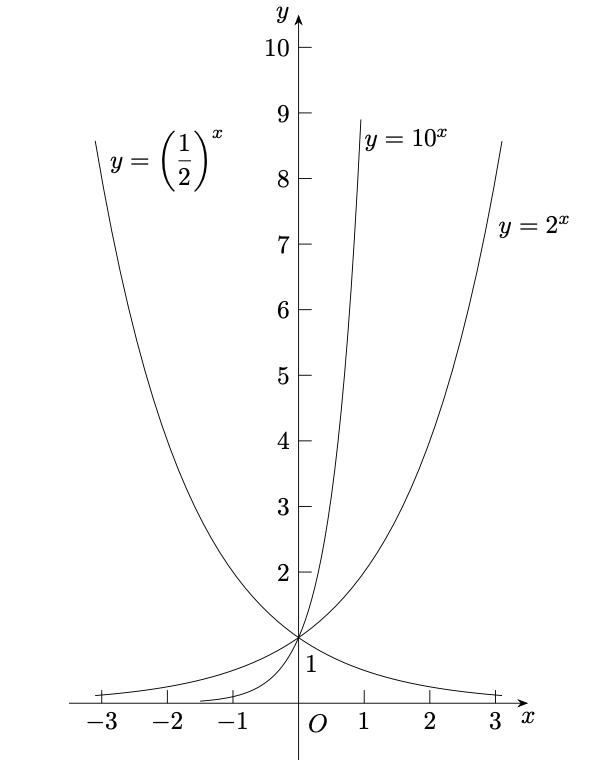
指数函数的图像有什么特点?(★★)
【核心结论】 图像特点取决于底数:
- 当时:
- 严格单调递增
- 图像从左到右上升越来越快
- 当时:
- 严格单调递减
- 图像从左到右下降越来越慢
【记忆技巧】
- :像”坐火箭”🚀,越飞越快
- :像”跳水”🏊,下降速度逐渐变慢
【概念地图】 底数 → 决定增减性 ↓ 导数 → 决定凹凸性 ↓ 应用 → 增长/衰减模型
提示
- 思考底数不同时的变化趋势
指数函数有哪些实际应用?(★★★)
【核心结论】 主要应用场景:
- 增长模型():
- 人口增长
- 细菌繁殖
- 复利计算
- 衰减模型():
- 放射性衰变
- 药物代谢
- 温度冷却
【记忆技巧】
- 增长模型:“滚雪球”📈越滚越大
- 衰减模型:“泄气球”📉越来越小
【应用公式】
- 复利计算:
- 衰变公式:
【关联考点】
- 对数函数(反函数)
- 指数方程
- 导数应用
提示
想想自然界中的快速增长现象
自然指数函数有什么特殊性质?(★★★)
【核心结论】 自然指数函数的特点:
- 底数
- 导数等于自身:
- 是最自然的指数增长模型
【记忆技巧】 “自己的导数是自己”:
- 像”自带永动机”的函数
- 变化率永远等于当前值
【重要性质】
- 在任意点的切线斜率等于该点的函数值
【应用场景】
- 连续复利计算
- 自然增长模型
- 微分方程
提示
思考它的导数特点
指数方程的基本类型有哪些?(★★)
【核心结论】 常见的指数方程类型:
- 同底指数方程:
- 变形同底方程:
- 异底指数方程:
- 复合函数型:(M为常数)
【记忆技巧】 像”变装舞会”:
- 同底:穿同样衣服👔
- 变形同底:同款不同色👕
- 异底:完全不同装扮👗
【解题思路】
- 先识别方程类型
- 转化为同底形式
- 利用指数函数的单调性
提示
观察等号两边的指数形式
如何解同底指数方程?(★★)
【核心结论】 解同底指数方程的步骤:
- 当时:
- 当时:
【思维脚手架】
- 检查底数的范围
- 利用指数函数的一一对应性质
- 直接令指数相等
- 解普通方程
【例题示范】 解方程:
- 底数
- 所以
- 解得
【易错警示】 ⚠️ 注意:
- 检查解是否在定义域内
- 别忘记验证最终答案
提示
利用指数函数的单调性
如何解异底指数方程?(★★★)
【核心结论】 解异底指数方程的方法:
-
换底法:两边取对数
-
同底化:找公共底数 如: 化为
【解题步骤】
- 判断是否可以同底化
- 不能同底化时使用换底法
- 解出x后代回验证
【例题示范】 解:
- 两边取ln:
- 得:(唯一解)
【关联考点】
- 对数运算法则
- 指数函数性质
- 换底公式
提示
尝试转化为同底形式
复合函数型指数方程怎么解?(★★★)
【核心结论】 解型方程步骤:
-
当时:
- 两边取对数:
- 解出:
-
当时:
- 无解(因为指数函数值域为正数)
【思维脚手架】
- 检查M的正负
- 利用对数化简
- 解普通方程
- 验证定义域
【例题示范】 解:
【易错警示】 ⚠️ 常见错误:
- 忘记检查M的范围
- 忘记验证解的定义域
- 遗漏正负号解
提示
观察指数部分的函数特征
指数不等式有什么基本性质?(★★)
【核心结论】 对于指数不等式:
- 当时:
- 保持不等号方向:
- 当时:
- 改变不等号方向:
【记忆技巧】
- :“大哥带大弟”(不等号方向不变)
- :“小弟反着来”(不等号方向相反)
【易错警示】 ⚠️ 解题前必须:
- 先判断底数范围
- 再决定不等号方向
提示
回忆指数函数的单调性
如何解基本指数不等式?(★★)
【核心结论】 解题步骤:
- 判断底数范围
- 确定不等号方向
- 解普通不等式
- 注意定义域限制
【思维脚手架】 例如:解
- 底数,不等号方向不变
- 答案:
【关联考点】
- 指数函数单调性
- 区间表示法
- 一元不等式解法
【易错警示】 ⚠️ 注意:
- 检查定义域
- 区间写法规范
- 验证临界点
提示
分析底数与不等号的关系
如何解异底指数不等式?(★★★)
【核心结论】 解型不等式:
- 换底法:
- 两边取对数(注意对数底数要大于0)
- 分类讨论:
- 当时:
- 当时:
【例题示范】 解:
- 两边取ln:
- 因,所以
- 答案:
【记忆技巧】 “正负号决定大小”:
- 正数乘大数更大
- 负数乘大数更小
提示
考虑对数转化方法
复合函数型指数不等式如何解?(★★★)
【核心结论】 解(M>0)型不等式:
-
当时:
-
当时:
【思维脚手架】 例如:解
【重要提示】 解题三步法:
- 化简指数
- 处理不等号
- 考虑定义域
【关联考点】
- 对数运算
- 区间交并集
- 二次不等式
提示
分解为基本步骤
分段函数型指数不等式有什么特点?(★★★)
【核心结论】 分段函数型指数不等式特点:
- 需要分区间讨论
- 注意分段点的连续性
- 最后结果需要取交集
【解题思路】
- 确定分段点
- 在每个区间上分别求解
- 检查分段点处的情况
- 合并所有解集
【记忆技巧】 像”拼图游戏”🧩:
- 每个区间是一块拼图
- 要检查拼图的接缝处
- 最后拼成完整图案
提示
注意分段点的连续性
如何解含绝对值的指数不等式?(★★★)
【核心结论】 解型不等式:
-
当时: 解
-
当时: 解
【思维脚手架】 例如:解
- 分类讨论:
- 当时:
- 当时:
- 解出:
- 或
- 或
- 答案:
【易错警示】 ⚠️ 注意:
- 分段点要取等
- 区间边界要验证
- 结果要取并集
提示
利用绝对值的分段性质
如何解max/min型指数不等式?(★★★)
【核心结论】 解或:
-
max型:
- 时,解
- 时,解
-
min型:
- 时,解
- 时,解
【解题步骤】
- 找出分段点:
- 分区间讨论
- 解各区间不等式
- 合并解集
【例题示范】 解:
- 分段点:,即
- 当时:
- 当时:
- 解得:
提示
将最大/最小值转化为分段函数
复杂分段函数型指数不等式的解题策略是什么?(★★★)
【核心结论】 解题策略:
- 化繁为简:
- 拆分为基本分段
- 逐段处理
- 分类讨论:
- 列出所有可能情况
- 分别求解
- 结果整合:
- 检查重叠区间
- 取交集或并集
【思维脚手架】
- 画出函数图像辅助分析
- 标注关键分段点
- 列表归纳所有情况
- 逐一求解后合并
【关联考点】
- 分段函数
- 指数函数性质
- 区间运算
- 函数图像
【易错警示】 ⚠️ 特别注意:
- 分段点的连续性
- 解集的开闭区间
- 定义域的限制
- 最终解的验证
提示
系统化分解复杂问题
含参数的指数不等式有什么特点?(★★★)
【核心结论】 含参数指数不等式的特点:
- 需要分类讨论参数范围
- 解集与参数之间有函数关系
- 要考虑参数对不等号方向的影响
【解题思路】
- 先观察参数位置:
- 在指数位置
- 在底数位置
- 在不等式右端
- 分析参数范围对解集的影响
- 列出不同情况下的解集
【记忆技巧】 像”变量天气”:
- 参数就是天气条件🌤️
- 解集就是相应对策☔
- 要”见招拆招”应对不同情况
提示
思考参数对不等式的影响
如何解指数位置含参数的不等式?(★★★)
【核心结论】 解(k为参数)型不等式:
- 当时:
- :
- :
- 当时:
- :
- :
【例题示范】 解:(k为参数)
- 因为,所以:
- 分类讨论:
- 当时:
- 当时:
- 当时:无解
【易错警示】 ⚠️ 注意:
- 参数为0的特殊情况
- 不等号方向的变化
- 解集的表示方法
提示
注意参数与变量的关系
如何解底数位置含参数的不等式?(★★★)
【核心结论】 解(m为参数)型不等式:
- 先确定底数范围:
- 要求
- 分类讨论:
- 当时:
- 当时:
【思维脚手架】 例如:解
- 条件:,即
- 分类:
- 当时:
- 当时:
- 当时:无解
【关联考点】
- 对数函数
- 参数范围
- 分类讨论
提示
分析参数对底数范围的影响
如何解复杂参数型指数不等式?(★★★)
【核心结论】 解题策略:
-
参数分析:
- 列出参数的可能取值范围
- 分析参数间的关系
-
条件转化:
- 化简为标准形式
- 提取关键不等式
-
分类讨论:
- 按参数范围分类
- 逐类求解
【例题示范】 解:(m,p为参数)
- 分析底数:
- 当时:
- 当时:
- 进一步分类:
- 时
- 时
- 时
【重要提示】 解题三步走:
- 化简参数式
- 分类讨论
- 合并结果
【易错警示】 ⚠️ 注意:
- 参数取值范围
- 特殊值情况
- 解集的表达
- 结果的验证
提示
系统化处理多参数情况
分段函数与参数结合的指数不等式有什么特点?(★★★)
【核心结论】 主要特点:
-
参数可能影响:
- 分段点的位置
- 分段函数的形式
- 不等式的解集
-
需要多重分类:
- 按参数范围分类
- 按分段条件分类
- 按不等式情况分类
【解题思路】
- 先分析参数对分段点的影响
- 确定参数的合理取值范围
- 在每个参数区间内分别处理分段情况
- 最后综合所有情况
【记忆技巧】 像”多重迷宫”🏰:
- 参数是入口选择
- 分段是路径选择
- 要找到每条通路
提示
思考参数如何影响分段点
如何解决分段点含参数的指数不等式?(★★★)
【核心结论】 解题步骤:
- 找出含参分段点
- 分析分段点的变化规律
- 确定参数对应的不同分段情况
- 在每种情况下解不等式
【例题示范】 解:,其中
- 分段点
- 分类讨论:
- 当时:
- 当时:
- 解得:
- 最后合并区间并考虑分段条件
【易错警示】 ⚠️ 注意:
- 分段点的连续性
- 解集的开闭区间
- 参数取值限制
提示
注意分段点随参数变化
如何处理分段函数形式受参数影响的情况?(★★★)
【核心结论】 解题策略:
- 参数影响分析:
- 参数改变函数形式
- 参数改变不等式性质
- 多重分类讨论:
- 按参数范围分类
- 按函数形式分类
- 按不等式性质分类
【例题示范】 解:,其中 (a>1, k为参数)
- 分析参数k:
- 影响部分的斜率
- 影响部分的平移
- 分类讨论:
- 当时:
- 当时:
【思维脚手架】
- 画图辅助分析
- 列表归纳情况
- 分别求解
- 检查连接处
提示
分析参数对函数形式的影响
复杂分段参数指数不等式的系统解法是什么?(★★★)
【核心结论】 系统解法步骤:
- 预处理阶段:
- 分析参数范围
- 确定分段条件
- 研究函数连续性
- 分类讨论阶段:
- 参数分类
- 区间分类
- 函数形式分类
- 求解阶段:
- 解每种情况
- 检查边界点
- 验证解的合理性
【解题技巧】
- 画图分析:
- 标注分段点
- 画出可能的函数图形
- 观察参数影响
- 表格整理:
- 列出所有情况
- 记录各种条件
- 归纳最终结果
【易错警示】 ⚠️ 特别注意:
- 参数取值范围
- 分段点连续性
- 解集的合理性
- 特殊值验证
提示
建立完整的解题框架
【例1】求解方程: (★★★)
【解题步骤】
-
将右边转化为2的幂:
-
利用指数方程性质:
-
整理为标准形式:
-
解得: 或
【解题要点】
- 转化为同底数
- 利用二次方程求解
- 验证解的合理性
【易错提醒】 ⚠️ 注意:
- 不要忘记验证定义域
- 检查指数是否有意义
提示
转化为同底指数方程
【例2】求解不等式: (★★★)
【解题步骤】
-
令,则
-
不等式转化为:
-
利用基本不等式: 对于任意正实数, 当且仅当时取等号
-
所以:恒成立 取等时:,即
-
解得:
【解题要点】
- 巧妙换元
- 利用基本不等式
- 理解取等条件
【关联知识】
- 基本不等式
- 指数函数性质
- 函数图像
提示
利用基本不等式
【例3】已知函数,,证明:对任意实数, (★★★)
【证明过程】
-
代入函数表达式:
-
利用指数运算法则:
-
因为为任意实数,所以对任意都成立
【证明要点】
- 清晰的逻辑步骤
- 运用指数运算法则
- 说明普遍性
【延伸思考】
- 函数图像的几何意义
- 复合函数的性质
- 反函数的关系
提示
代入函数表达式
【例4】某细菌在适宜条件下每小时分裂一次,初始有100个细菌,求:
- 2小时后的细菌数量
- 多少小时后细菌数量达到6400个 (★★★)
【解题步骤】
-
建立模型: (t为小时数)
-
求2小时后数量: (个)
-
求达到6400个时的时间:
【解题要点】
- 准确建立模型
- 代入求解
- 利用指数方程
【实际意义】
- 检查答案合理性
- 理解指数增长含义
- 注意实际约束条件
【易错提醒】 ⚠️ 注意:
- 单位统一
- 数量为整数
- 时间为非负数
提示
建立指数增长模型
【例5】求解参数方程:,其中,求参数的取值范围。(★★★)
【解题步骤】
-
分析函数:
- 左边为指数函数
- 右边为直线
- 方程有解表示两函数有交点
-
利用导数:
- 的导数为
- 直线斜率为
- 切点处导数相等
-
求解: 设切点为
- 消元得:
-
结论:
【解题要点】
- 利用导数判断切点
- 建立方程组
- 分析参数范围
【易错提醒】 ⚠️ 注意:
- 参数的合理性
- 函数的单调性
- 解的存在性
提示
考虑指数函数与线性函数的交点
【例6】解不等式组: (★★★)
【解题步骤】
-
由分类讨论:
- 第一象限:
- 第三象限:
-
第一象限时:
- 无解(因为)
-
第三象限时:
- 解得: 且满足
【解题要点】
- 分类讨论
- 考虑函数性质
- 注意定义域
【图形意义】
- 在坐标平面上画图
- 理解不等式几何意义
提示
分类讨论xy的符号
【例7】已知函数 求函数的单调区间。(★★★)
【解题步骤】
-
分段点处:
- 左极限:
- 右极限:
- 函数在处连续
-
导数分析: 当时: 当时:
-
单调性:
- 当时: 时递减 时递增
- 处导数不存在,但函数连续
-
结论: 递减区间: 递增区间:
【解题要点】
- 分段点连续性
- 导数判断单调性
- 特殊点处理
【易错提醒】 ⚠️ 注意:
- 分段点的连续性
- 导数不存在点
- 区间的开闭
提示
分段函数分别讨论
【例8】某放射性物质每24小时衰变为原来的四分之一,若初始量为32克,求:
- t小时后的剩余量
- 剩余8克时经过的时间 (★★★)
【解题步骤】
-
建立模型:
- 24小时衰变为
- 设小时后剩余量为
-
求剩余8克时间: (小时)
【解题要点】
- 建立正确模型
- 化简指数表达式
- 解指数方程
【实际应用】
- 理解半衰期概念
- 掌握衰变规律
- 应用于实际问题
【易错提醒】 ⚠️ 注意:
- 时间单位统一
- 量的实际意义
- 结果的合理性
提示
建立指数衰减模型
【错误类型1】指数运算错误分析 (★★★)
【典型错误】
-
指数加减错误: ❌ ✅
-
负指数处理错误: ❌ ✅
-
分数指数错误: ❌ ✅
【错误原因】
- 混淆代数运算法则
- 忽视指数运算特点
- 理解概念不深入
【纠正方法】
-
牢记基本法则:
-
多做练习,加深理解
提示
总结常见的运算错误
【错误类型2】定义域判断错误分析 (★★★)
【典型错误】
-
底数为负: ❌ 的定义域为 ✅ 只在为整数时有意义
-
复合函数定义域: ❌ 的定义域为 ✅ 定义域为
-
分式指数: ❌ 的定义域为 ✅ 定义域为
【错误原因】
- 忽视底数限制
- 忽略内层函数定义域
- 未考虑特殊点
【检查方法】
-
底数检查:
- 底数必须为正数
- 特殊底数要特别注意
-
复合函数检查:
- 内层函数定义域
- 外层函数要求
提示
注意指数函数的定义域特点
【错误类型3】方程解答错误分析 (★★★)
【典型错误】
-
遗漏解: ❌ 只有 ✅ 解应为
-
无效解: ❌ 有解 ✅ 指数函数值恒为正,无解
-
对数转化错误: ❌ → ✅ 应为 →
【错误原因】
- 未考虑对称性
- 忽视值域限制
- 转化过程不严谨
【解决方法】
-
验证步骤:
- 代入检验
- 考虑对称性
- 检查定义域
-
注意事项:
- 指数函数值域
- 方程等价性
- 解的合理性
提示
分析解方程常见错误
【错误类型4】不等式解答错误分析 (★★★)
【典型错误】
-
不等号方向: ❌ → ✅ →
-
区间表示: ❌ → ✅ → ,写作
-
分类讨论遗漏: ❌ 无需讨论 ✅ 指数函数恒正,解集为
【错误原因】
- 忽视底数大小影响
- 区间表示不规范
- 条件分析不充分
【改正方法】
-
解题步骤:
- 判断底数范围
- 确定不等号方向
- 规范表示解集
-
检查要点:
- 解的合理性
- 区间的开闭
- 特殊点处理
【预防措施】
-
画图辅助:
- 理解函数性质
- 判断解的范围
- 验证结果
-
多方验证:
- 代入检验
- 边界检查
- 实际意义
提示
总结不等式解答常见错误
【错误类型5】函数性质判断错误分析 (★★★)
【典型错误】
-
单调性判断: ❌ 在上单调递增 ✅ 在上单调递减
-
奇偶性判断: ❌ 是奇函数 ✅ 既不是奇函数也不是偶函数
-
周期性判断: ❌ 的周期是 ✅ 的周期是
【错误原因】
- 混淆函数性质
- 复合函数理解不深
- 性质判断不严谨
【纠正方法】
-
严格定义验证:
- 单调性:比较和
- 奇偶性:验证和
- 周期性:验证
-
画图辅助理解
提示
分析函数性质判断中的常见错误
【错误类型6】参数问题错误分析 (★★★)
【典型错误】
-
参数范围遗漏: ❌ 中可以为任意正数 ✅ 需要且
-
参数讨论不全: ❌ 只讨论 ✅ 还需讨论的取值范围
-
特殊值遗漏: ❌ 忽略参数为0或1的情况 ✅ 特殊值往往是关键点
【错误原因】
- 参数分析不充分
- 特殊情况遗漏
- 条件理解片面
【解决策略】
-
参数分析步骤:
- 列出参数条件
- 分类讨论
- 考虑特殊值
- 验证结果
-
图形辅助:
- 画出函数族
- 观察变化规律
提示
总结含参数问题的常见错误
【错误类型7】应用题建模错误分析 (★★★)
【典型错误】
-
模型选择错误: ❌ 所有增长都用指数模型 ✅ 需分析具体增长方式
-
单位换算错误: ❌ 忽视时间单位统一 ✅ 注意单位换算关系
-
实际意义错误: ❌ 得到负值仍保留 ✅ 考虑实际可能性
【错误原因】
- 模型理解不准
- 实际意义忽视
- 数据处理不当
【改正方法】
-
建模步骤:
- 分析实际情况
- 选择合适模型
- 确定变量关系
- 检验合理性
-
结果验证:
- 单位统一
- 数值合理
- 实际意义
提示
分析实际应用题中的建模错误
【错误类型8】证明题错误分析 (★★★)
【典型错误】
-
证明不完整: ❌ 只证明部分情况 ✅ 需要考虑所有可能
-
逻辑推理错误: ❌ → (未考虑底数) ✅ 需考虑底数大小影响
-
结论推广错误: ❌ 特例正确就认为普遍正确 ✅ 需要严格的普遍性证明
【错误原因】
- 证明思路不清
- 逻辑链条断裂
- 条件使用不当
【改进方法】
-
证明规范:
- 明确已知条件
- 列出证明目标
- 逐步严格推导
- 考虑完整性
-
常用技巧:
- 反证法
- 数学归纳
- 分类讨论
- 作图辅助
【注意事项】
- 证明的完整性
- 推理的严谨性
- 结论的普遍性
- 特例的局限性
提示
分析数学证明中的常见错误
【2023年全国卷】已知函数。 (1) 求的最小值; (2) 求方程的解个数与的关系。 (★★★)
【解题步骤】
-
求导数:
-
令:
-
求最小值: 代入 得最小值为
-
方程解个数:
- 当小于最小值时,无解
- 当等于最小值时,一个解
- 当大于最小值时,两个解
【考点分析】
- 导数应用
- 单调性分析
- 方程解个数
【易错提醒】 ⚠️ 注意:
- 导数零点唯一性
- 最小值计算准确性
- 分类讨论完整性
提示
利用导数求最值和单调性
【2022年全国卷】设函数 求函数的值域。(★★★)
【解题步骤】
-
分析连续性: 在处不连续
-
分段讨论:
- 当时:,值域为
- 当时:,值域为
-
合并值域:
【考点分析】
- 分段函数
- 连续性
- 值域合并
【解题技巧】
- 画图辅助理解
- 注意分段点
- 考虑函数性质
提示
分段函数分别讨论
【2021年全国卷】解不等式: (★★★)
【解题步骤】
-
提取公因式:
-
求解:
-
答案:
【考点分析】
- 指数不等式
- 因式分解
- 区间表示
【易错提醒】 ⚠️ 注意:
- 不要忘记提取公因式
- 注意不等号方向
- 区间表示规范
【解题技巧】
- 化简为标准形式
- 利用指数性质
- 验证解的合理性
提示
提取公因式
【2020年全国卷】已知函数,。 (1) 求的值; (2) 证明:对任意,恒有。 (★★★)
【解题步骤】
-
求:
-
证明:
- 由对数定义:
- 所以
【考点分析】
- 复合函数
- 指数对数关系
- 不等式证明
【解题技巧】
- 逐步代入计算
- 利用定义转化
- 注意定义域
【易错提醒】 ⚠️ 注意:
- 复合顺序
- 对数运算
- 定义域限制
提示
理解复合函数与函数不等式
【2023北京卷】已知函数,其中且。 (1) 若有最小值,求的取值范围; (2) 当时,求的最小值。 (★★★)
【解题步骤】
-
求导数:
-
令:
-
分析范围:
- 要有最小值,必须有解
- 所以(使)
-
当时:
- 解得
- 代入原函数得最小值为
【考点分析】
- 参数讨论
- 导数应用
- 最值问题
【易错提醒】 ⚠️ 注意:
- 参数范围的严格推导
- 导数零点的存在性
- 最值的验证
提示
利用导数判断极值
【2023浙江卷】设函数,。 (1) 证明:存在,使得; (2) 求这样的的值。 (★★★)
【解题步骤】
-
证明存在性:
- 令
- 由零点定理,存在使
-
求值:
- 令代入验证
- 得
- 令代入验证成立
【考点分析】
- 零点定理
- 方程求解
- 验证方法
【解题技巧】
- 构造辅助函数
- 利用零点定理
- 尝试特殊值
提示
利用连续性和单调性
【2023上海卷】已知函数 在处连续,求和的值。(★★★)
【解题步骤】
-
连续性条件:
-
代入: (右极限为1)
-
可导性条件:
-
验证: ,时函数在处连续可导
【考点分析】
- 分段函数连续性
- 导数连续性
- 参数确定
【易错提醒】 ⚠️ 注意:
- 左右极限相等
- 导数存在条件
- 验证完整性
提示
利用函数连续性条件
【2023江苏卷】解不等式: (★★★)
【解题步骤】
-
分类讨论:
- 当时:
- 当时:
-
解第一种情况:
-
解第二种情况:
-
合并结果:
【考点分析】
- 绝对值不等式
- 指数不等式
- 区间表示
【解题技巧】
- 分类讨论
- 分别求解
- 合并区间
【易错提醒】 ⚠️ 注意:
- 分类点的取值
- 不等号方向
- 解集的表示
提示
分类讨论绝对值