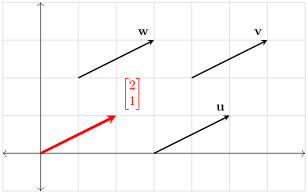
向量

形式定义

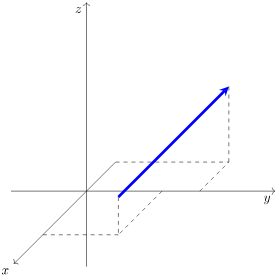
向量是同时具有大小和方向的量，可以在实数空间 ${\mathbb{R}}^n$ 中表示为有序 $n$ 元组： $\vec{a}=(a_1,a_2,\dots ,a_n)$ 其中 $a_1,a_2,\dots ,a_n$ 是向量的分量。

直观解释

• 几何表示：从起点指向终点的有向线段
• 物理表示：具有大小和方向的物理量（如位移、速度、力等）
• 代数表示：有序数组或 $n$ 维空间中的点

符号表示

• 向量符号：$\vec{a}$、$\mathbf{a}$、$\underline{a}$ 或粗体 $\mathbf{a}$
• 向量模长：$|\vec{a}|$ 或 $\Vert \vec{a}\Vert$
• 单位向量：$\hat{a}$ 或 ${\vec{a}}^0$（模长为1的向量）
• 零向量：$\vec{0}$ 或 $0$（所有分量为0的向量）

1. 向量相等：两个向量相等当且仅当它们的对应分量相等 $\vec{a}=\vec{b}⟺a_i=b_i\text{ 对所有 }i=1,2,\dots ,n$

2. 向量加法：分量对应相加 $\vec{a}+\vec{b}=(a_1+b_1,a_2+b_2,\dots ,a_n+b_n)$

3. 标量乘法：所有分量乘以同一个标量 $k\vec{a}=(k{a}_1,k{a}_2,\dots ,k{a}_n)$

4. 向量的模长： $|\vec{a}|=\sqrt{a_1^2+a_2^2+\dots +a_n^2}$

重要定理

1. 向量加法的交换律：$\vec{a}+\vec{b}=\vec{b}+\vec{a}$
2. 向量加法的结合律：$(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$
3. 标量乘法的分配律：$k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$
4. 标量乘法的结合律：$(kl)\vec{a}=k(l\vec{a})$

关键公式

1. 向量点积（内积）： $\vec{a}\cdot \vec{b}=a_1{b}_1+a_2{b}_2+\dots +a_n{b}_n=|\vec{a}||\vec{b}|\cos \theta$ 其中 $\theta$ 是两向量间的夹角

2. 向量叉积（仅在三维空间中定义）： $\vec{a}\times \vec{b}=(a_2{b}_3-a_3{b}_2,a_3{b}_1-a_1{b}_3,a_1{b}_2-a_2{b}_1)$ 叉积的模长等于 $|\vec{a}||\vec{b}|\sin \theta$，方向垂直于 $\vec{a}$ 和 $\vec{b}$ 所在平面

3. 单位向量： $\hat{a}=\frac{\vec{a}}{|\vec{a}|}$

特殊情况

1. 平行向量：两非零向量 $\vec{a}$ 和 $\vec{b}$ 平行，当且仅当存在非零实数 $k$ 使得 $\vec{a}=k\vec{b}$
2. 正交向量：两向量 $\vec{a}$ 和 $\vec{b}$ 正交，当且仅当 $\vec{a}\cdot \vec{b}=0$
3. 线性相关：一组向量线性相关，当且仅当其中至少一个向量可以表示为其他向量的线性组合

1. 三角不等式：对任意向量 $\vec{a}$ 和 $\vec{b}$，有 $|\vec{a}+\vec{b}|\le |\vec{a}|+|\vec{b}|$
2. 柯西-施瓦茨不等式：$|\vec{a}\cdot \vec{b}|\le |\vec{a}||\vec{b}|$
3. 向量投影：$\vec{a}$ 在 $\vec{b}$ 方向上的投影长度为 ${\text{proj}}_{\vec{b}}\vec{a}=\frac{\vec{a}\cdot \vec{b}}{|\vec{b}|}$

实际应用

1. 物理学：描述力、速度、加速度等物理量
2. 计算机图形学：三维建模、动画和游戏开发
3. 机器学习：特征向量表示和数据分析
4. 工程学：结构分析、电路设计

跨领域联系

1. 与线性代数的联系：向量是线性空间的元素
2. 与微积分的联系：向量微积分（梯度、散度、旋度）
3. 与几何学的联系：向量方法解决几何问题
4. 与力学的联系：力的合成与分解

例题1：判断向量 $\vec{a}=(2,-1,3)$ 和 $\vec{b}=(4,2,-1)$ 是否正交。

解析：

• 两向量正交当且仅当它们的点积为零
• 计算点积：$\vec{a}\cdot \vec{b}=2\times 4+(-1)\times 2+3\times (-1)=8-2-3=3\ne 0$
• 结论：这两个向量不正交

例题2：已知向量 $\vec{a}=(1,2,3)$ 和 $\vec{b}=(2,0,-1)$，求 $\vec{a}$ 在 $\vec{b}$ 方向上的投影向量。

解析：

1. 向量 $\vec{a}$ 在 $\vec{b}$ 方向上的投影长度为： ${\text{proj}}_{\vec{b}}\vec{a}=\frac{\vec{a}\cdot \vec{b}}{|\vec{b}|}=\frac{1\times 2+2\times 0+3\times (-1)}{|\vec{b}|}=\frac{2-3}{\sqrt{2^2+0^2+(-1{)}^2}}=\frac{-1}{\sqrt{5}}$

2. 投影向量 = 投影长度 × $\vec{b}$ 的单位向量： ${\text{proj}}_{\vec{b}}\vec{a}\cdot \frac{\vec{b}}{|\vec{b}|}=\frac{-1}{\sqrt{5}}\cdot \frac{(2,0,-1)}{\sqrt{5}}=\frac{-1}{5}(2,0,-1)=(-\frac{2}{5},0,\frac{1}{5})$

例题3：证明拉格朗日恒等式：对任意三维向量 $\vec{a}$ 和 $\vec{b}$，有 $|\vec{a}\times \vec{b}{|}^2=|\vec{a}{|}^2|\vec{b}{|}^2-(\vec{a}\cdot \vec{b}{)}^2$

解析：

1. 设 $\vec{a}=(a_1,a_2,a_3)$ 和 $\vec{b}=(b_1,b_2,b_3)$
2. 计算叉积：$\vec{a}\times \vec{b}=(a_2{b}_3-a_3{b}_2,a_3{b}_1-a_1{b}_3,a_1{b}_2-a_2{b}_1)$
3. 计算叉积的模长平方： $|\vec{a}\times \vec{b}{|}^2=(a_2{b}_3-a_3{b}_2{)}^2+(a_3{b}_1-a_1{b}_3{)}^2+(a_1{b}_2-a_2{b}_1{)}^2$
4. 展开并整理： $|\vec{a}\times \vec{b}{|}^2=(a_2^2{b}_3^2+a_3^2{b}_2^2-2a_2{a}_3{b}_2{b}_3)+(a_3^2{b}_1^2+a_1^2{b}_3^2-2a_1{a}_3{b}_1{b}_3)+(a_1^2{b}_2^2+a_2^2{b}_1^2-2a_1{a}_2{b}_1{b}_2)$
5. 计算 $|\vec{a}{|}^2|\vec{b}{|}^2-(\vec{a}\cdot \vec{b}{)}^2$： $|\vec{a}{|}^2|\vec{b}{|}^2=(a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2)$ $(\vec{a}\cdot \vec{b}{)}^2=(a_1{b}_1+a_2{b}_2+a_3{b}_3{)}^2$
6. 展开并比较两式，可以证明它们相等

错误类型：混淆向量的点积和叉积

• 错误理解：认为两个向量的点积也是一个向量
• 正确理解：点积结果是标量，叉积结果是向量