card
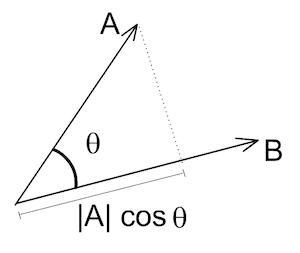
如何证明向量内积的几何定义和代数定义相等? 即:a·b = |a||b|cosθ = x₁x₂ + y₁y₂ + z₁z₂
- 考虑使用余弦定理
- 注意箭头方向,why?
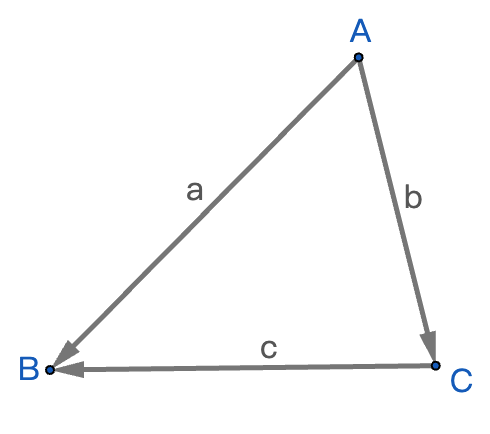
- 参考三角形的向量表示
证明思路:
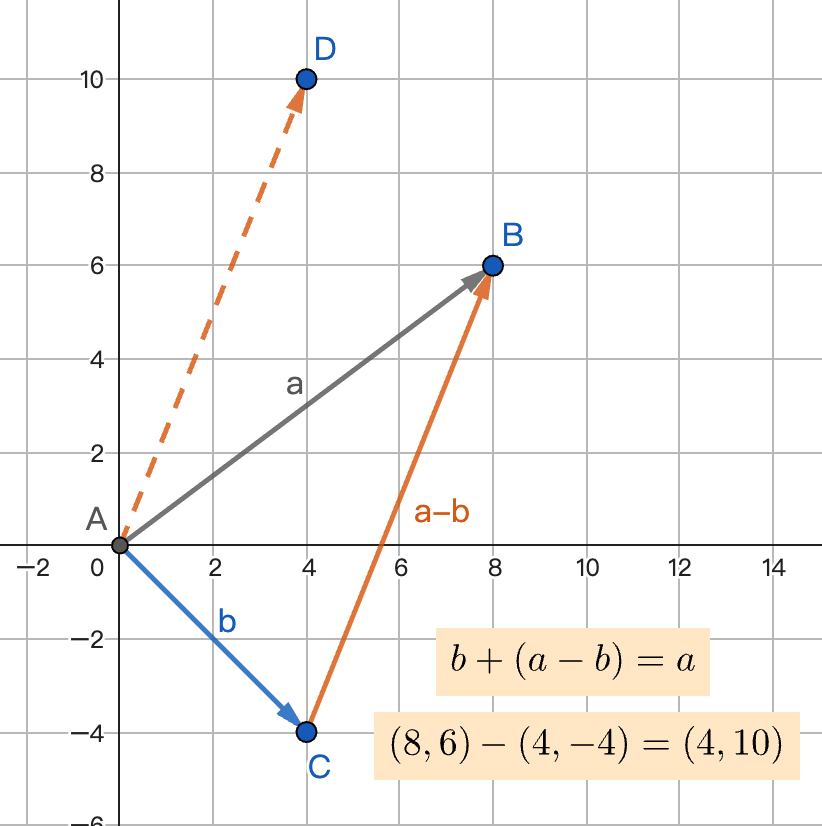
- 利用向量减法和模长
- 应用余弦定理
- 展开代数式
具体步骤:
-
设 c = a - b,则 |c|² = (a-b)·(a-b)
-
根据余弦定理: |c|² = |a|² + |b|² - 2|a||b|cosθ
-
展开(a-b)·(a-b): |c|² = (x₁-x₂)² + (y₁-y₂)² + (z₁-z₂)² = (x₁² + y₁² + z₁²) + (x₂² + y₂² + z₂²) - 2(x₁x₂ + y₁y₂ + z₁z₂) = |a|² + |b|² - 2(x₁x₂ + y₁y₂ + z₁z₂)
-
由2)和3)相等: |a|² + |b|² - 2|a||b|cosθ = |a|² + |b|² - 2(x₁x₂ + y₁y₂ + z₁z₂)
-
因此: |a||b|cosθ = x₁x₂ + y₁y₂ + z₁z₂
提示
-
考虑使用余弦定理
-
注意箭头方向,why?

-
参考三角形的向量表示
card
这个证明的关键点和启示是什么?
思考证明的核心思路
关键点:
- 巧用向量减法构造新向量
- 余弦定理桥接几何和代数
- 模长的两种表达方式
启示:
- 几何问题可转化为代数
- 余弦定理是重要工具
- 向量运算的等价性
提示
思考证明的核心思路
card
这个证明方法还可以用在哪些场合?
思考类似的证明情境
应用场景:
- 证明其他向量运算的等价定义
- 建立几何量与代数量的关系
- 验证向量空间的性质
- 推导新的向量恒等式
- 解决向量几何问题
提示
思考类似的证明情境