card
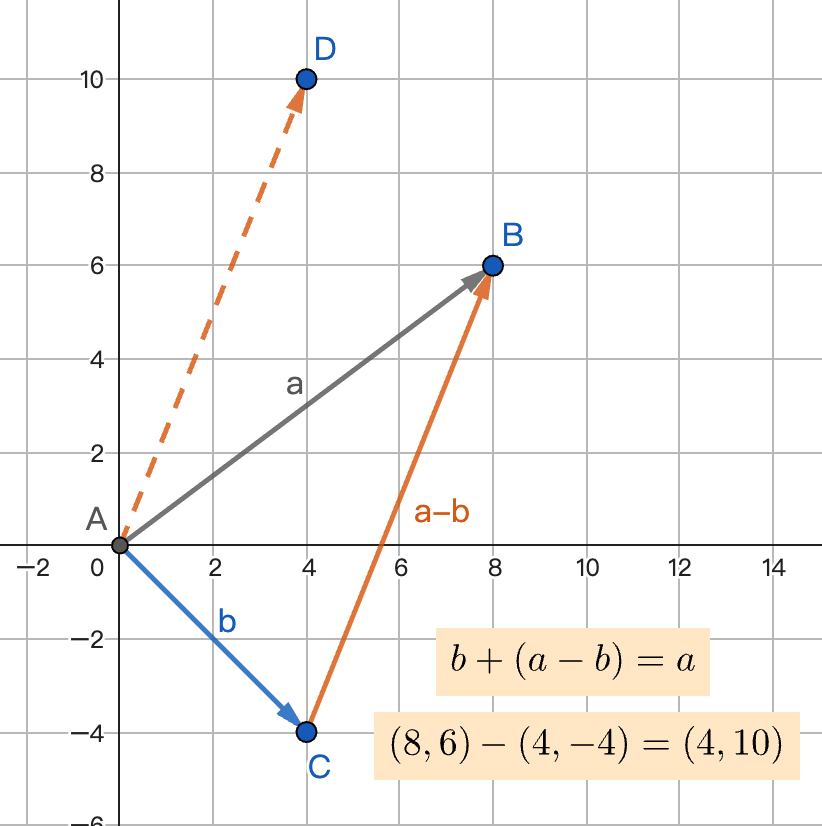
三角形ABC中,向量关系是如何表示的?
思考向量的起点和终点
- 向量减法即加上相反向量
- 路径必须首尾相连
- 起点终点决定结果向量
- 中间路径虽然不同,但等效结果相同
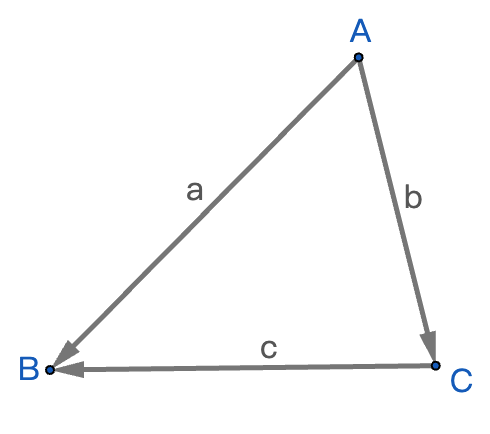
- 向量表示:
- a:从A指向B的向量
- b:从A指向C的向量
- c:从C指向B的向量(或说从B指向C的负向量)
- 关系解释:
- 先到C
- 再返回A(-b)
- 最后到B(向量a)
- 等价于直接从C到B()
提示
思考向量的起点和终点
- 向量减法即加上相反向量
- 路径必须首尾相连
- 起点终点决定结果向量
- 中间路径虽然不同,但等效结果相同

card
这个向量关系能推导出哪些三角形性质?
考虑向量模长和点积
- 余弦定理:
- 三角形面积:
- 中线定理:
中线长度
提示
考虑向量模长和点积
card
这种向量表示法有什么优势?
思考计算和理解的便利性
优势:
-
统一性:
- 把三角形所有边统一到向量关系中
- 便于推导各种性质
-
简洁性:
- 一个式子c=a-b包含全部信息
- 运算规则清晰直观
-
推广性:
- 容易推广到空间
- 便于处理复杂几何问题
提示
思考计算和理解的便利性
card
用向量方法解决三角形问题的关键是什么?
思考向量的基本运算
关键点:
-
建立向量关系:
- 正确选择向量方向
- 确定向量起终点
-
运用向量运算:
- 点积求夹角和长度
- 叉积求面积
- 向量加减求位置关系
-
几何意义:
- 向量运算对应几何关系
- 保持几何直观
提示
思考向量的基本运算
card
如何用这个向量关系解决具体问题?
考虑一个实际例子
例:证明三角形中线长公式
解:
- 设M是BC中点,AM是中线
- M的位置向量:(B+C)/2
- 中线向量:AM = M-A
- 代入c=a-b: M-A = ½(B-A) - ½(C-A) = ½(a-b)
- 平方得中线长公式: m² = ¼(2a² + 2b² - c²)
提示
考虑一个实际例子