基本定义
形式定义
实数空间通常记作 ,表示由 个实数组成的所有有序 元组的集合:
直观解释
- 即实数轴
- 是平面直角坐标系
- 是三维空间
- 更高维度的实数空间虽然难以直观想象,但可以用代数方式严格定义和处理
符号表示
- 点: 或向量
- 原点:
核心性质
基本性质
- 线性结构: 是线性空间(向量空间),满足向量加法和标量乘法运算
- 度量结构:通过距离函数定义点之间的距离
- 拓扑结构:具有开集、闭集、连通性等拓扑性质
重要定理
-
毕达哥拉斯定理推广: 中两点 和 之间的距离为:
-
柯西-施瓦茨不等式:对任意 ,有:
关键公式
- 向量的模长:
- 点积:
- 两向量夹角:
概念推论
直接推论
- 三角不等式:对任意 ,有
- 平行向量:两非零向量平行当且仅当存在非零实数 使得
- 正交向量:两向量正交当且仅当它们的点积为零,即
实际应用
- 物理学:描述物体在空间中的位置、速度、加速度等
- 计算机图形学:三维建模、计算机动画
- 数据分析:多维数据的表示和处理
- 机器学习:特征空间的构建
典型例题
基础例题(概念理解型)
例题1:判断向量 和 是否正交。
解析:
- 思路:两向量正交当且仅当它们的点积为零
- 计算点积:
- 结论:这两个向量不正交
中等例题(多步骤型)
例题2:在 中,求点 到平面 的距离。
解析:
- 平面的法向量为
- 平面上任取一点,如 (令 求得)
- 向量
- 点到平面的距离公式:
- 计算:
挑战例题(思维拓展型)
例题3:证明 中任意 个向量线性相关。
解析:
- 假设有 个向量
- 考虑线性方程组
- 这是一个有 个未知数和 个方程的齐次线性方程组
- 根据线性代数理论,当未知数个数大于方程个数时,方程组必有非零解
- 因此存在不全为零的 使得
- 根据线性相关的定义,这 个向量线性相关
常见错误(概念混淆型)
错误类型:混淆向量的模长和维度
- 错误理解:认为向量 的模长是 4
- 正确理解:向量 的维度是 4,模长是
思维方法
思维方法
- 代数与几何结合:实数空间中的问题既可以用代数方法(坐标、方程)也可以用几何方法(距离、角度)解决
- 降维思考:复杂的高维问题可以通过投影或截面降到低维空间中考虑
- 类比推广:许多平面和三维空间的结论可以推广到高维空间
数学思想
- 抽象思维:从具体的空间概念抽象出维度更高的空间
- 公理化思维:通过公理系统严格定义实数空间的性质
- 不变量思想:研究在某些变换下保持不变的量(如距离、夹角等)
-
一维空间:
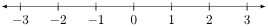
-
二维空间:

-
三维空间:

通过掌握实数空间的概念和性质,你将能够更好地理解高等数学中的多元函数、向量分析和线性代数等内容,为后续学习奠定坚实基础。
下一节:距离公式

