概念本质
正交向量是指相互垂直的向量,它们之间的夹角为90度(或π/2弧度)。正交性是向量空间中的一种基本几何关系,表示两个方向完全独立,没有任何一个向量在另一个向量方向上的分量。
数学定义
1. 点积定义 和 正交,当且仅当它们的点积为零:
两个非零向量
2. 坐标形式 和 ,则正交条件为:
若
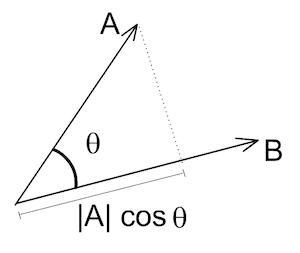
3. 几何解释 由于 和 非零,所以 ,即
正交向量的点积为零等价于:
重要性质
1. 基本性质
- 零向量与任何向量正交
- 向量与自身不正交(除非是零向量)
- 如果 ,则 (正交关系是对称的)
- 如果 ,则 ,其中 为任意非零实数
2. 勾股定理推广
若 ,则:
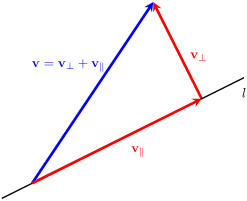
3. 正交分解
任何向量 可以分解为平行于向量 和正交于向量 的两个分量:
其中:
标准正交基
1. 定义
一组向量 构成标准正交基,如果:
- 它们两两正交: 当
- 它们都是单位向量:
2. 欧几里得空间中的标准正交基
三维空间中的标准正交基(直角坐标系):
应用实例
1. 物理学中的功
当力 与位移 正交时,力不做功:
2. 计算机图形学
- 计算法向量与表面的关系
- 实现镜面反射
// 计算反射向量
Vector3 Reflect(Vector3 incident, Vector3 normal) {
return incident - 2 * Vector3.Dot(incident, normal) * normal;
}
正交向量
正交性是一种强大的数学工具,它使复杂系统能够分解为简单的、相互独立的部分。从几何直观的垂直关系,到抽象空间中的独立性,正交性概念贯穿了现代数学和应用科学的核心。