单位向量逻辑🗡️

graph TD
    subgraph 核心概念递进
        A1[向量大小] -->|归一化| A2[单位向量]
        A2 -->|点积| A3[夹角余弦]
        A2 -->|叉积| A4[垂直方向]
    end
    
    subgraph 几何意义
        B1[方向表示] -->|单位圆| B2[三角函数]
        B2 -->|参数化| B3[cosθ,sinθ]
        B3 -->|复平面| B4[e^iθ]
    end
    
    subgraph 应用层次
        C1[坐标基底] -->|标准化| C2[方向度量]
        C2 -->|运算| C3[角度计算]
        C3 -->|推广| C4[高维空间]
    end

    A2 --> B1
    B3 --> C2

[A] 单位向量定义：模长等于1的向量，即 $∣ u ∣ = 1$
[B] 向量归一化：任意非零向量 $a$ 可转化为单位向量{{ $\overset{a}{^} = \frac{a}{∣ a ∣}$ }}
[C] 单位向量保持原向量方向，仅将其大小标准化为1
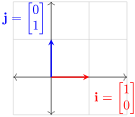
[D] 直角坐标系中的标准单位向量： $i = (1, 0, 0)$ , $j = (0, 1, 0)$ , $k = (0, 0, 1)$
[E] 单位向量的点积： $u \cdot v = cos θ$ ，其中 $θ$ 为两单位向量间的夹角
[F] 单位向量的叉积： $∣ u \times v ∣ = sin θ$ ，且 $u \times v$ 是垂直于 $u$ 和 $v$ 的单位向量
[G] 单位向量自身的点积： $u \cdot u = 1$ ，这是单位向量的自反性质
[H] 二维平面中的单位向量表示：任意二维单位向量可表示为 $u = (cos θ, sin θ)$ ，其中 $θ$ 是向量与x轴正方向的夹角

概念逻辑

单位向量概念本质

***：单位向量实现了向量两个基本属性——方向与大小的完美分离。这种解耦使我们能够在需要时单独处理方向信息，是现代向量分析的基础思想之一。表达式 $a = ∣ a ∣ \overset{a}{^}$ 不仅是一个数学等式，更是一种思维方法，它教导我们将复杂问题分解为***和***两个独立部分。
几何空间的标准化表达：单位向量为描述空间方向提供了标准化语言。无论空间维度多高，方向的表达总可归结为***上的点。这种标准化不仅简化了方向的数学处理，更为比较不同方向提供了统一的度量框架。
角度度量的代数化：单位向量间的点积直接给出***，这一性质将几何中的角度概念转化为代数运算，是向量代数与欧几里得几何深度融合的典范。
三角函数与向量的统一：命题H揭示了单位向量与三角函数的深刻联系——二维单位向量 $(cos θ, sin θ)$ 本质上是将角度 $θ$ 映射到***上的点。这一表示形式统一了三角函数和向量这两个看似独立的数学概念，揭示了它们在表达方向时的等价性。
参数化表示的典范：表达式 $(cos θ, sin θ)$ 是用单一参数 $θ$ 描述单位圆上所有点的典范案例，体现了参数化表示在数学中的强大作用。

单位向量的深层价值不仅在于它简化了向量计算，更在于它提供了一种思考空间关系的纯粹方式。通过单位向量，我们能够将注意力集中在***这一抽象概念上，而不受大小变化的干扰。特别是通过 $(cos θ, sin θ)$ 表示，单位向量成为连接欧几里得几何、三角学、复分析和群论的桥梁，体现了数学中不同分支间的深刻统一性。

概念推理余弦的向量定义

单位向量逻辑🗡️

概念逻辑

单位向量概念本质

一级链接

单位向量

home