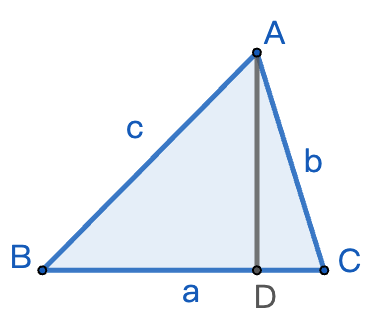
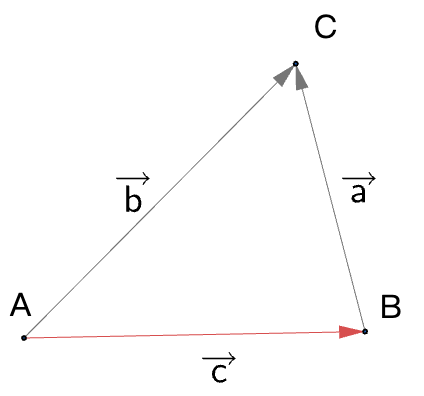
一般三角形可以通过在其内部作高线分解为两个直角三角形,这种方法引导出了一系列重要定理,包括正弦定理、余弦定理、面积公式、中线定理以及海伦公式等,形成了一个从基本到复杂的三角学知识体系。
余弦定理
在任意三角形 ABC 中,对于任意一边 a 和其对角 A,有: a² = b² + c² - 2bc cos A 其中 b 和 c 是三角形的另外两边。 同理: b² = a² + c² - 2ac cos B c² = a² + b² - 2ab cos C
余弦定理的特殊情况
当 A = 90°时,cos A = 0,余弦定理简化为: a² = b² + c² 这正是勾股定理,说明余弦定理是勾股定理的推广,或者说勾股定理是余弦定理的特例。
余弦定理及其推论体系
一级定理(基本形式)
余弦定理:在任意三角形ABC中
二级推论
- 角的余弦值表达
- 中线长公式
三级推论
- 三角形判定
- 当时,为锐角
- 当时,为直角
- 当时,为钝角
- 面积推论
- (海伦公式)
深层联系
- 与勾股定理的联系
- 当角为90°时,,退化为勾股定理
- 体现了特殊到一般的数学思想
- 与向量的联系
- 可以用向量点积证明余弦定理
- 体现了几何与代数的统一
- 与其他定理的联系
- 与正弦定理互补
- 可导出海伦公式
- 与中线定理相关
给定三边长,如何判断三角形是锐角、直角还是钝角三角形?
你想到了吗?和勾股定理有些关系?