正弦定理

概念定义

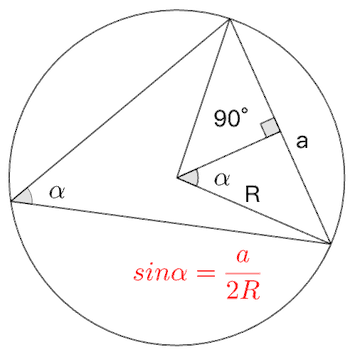
在任意三角形中，各边长与其对角正弦值的比值相等，且等于该三角形外接圆的直径。即： $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$ 其中$a$、$b$、$c$为三角形三边长，$A$、$B$、$C$为对应的三个内角，$R$为三角形外接圆半径。

定义等价性

• 基本形式：$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$
• 外接圆形式：$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
• 面积联系：$\text{面积}=\frac{1}{2}ab\sin C=\frac{1}{2}bc\sin A=\frac{1}{2}ac\sin B$
• 反向表达：$a=2R\sin A$，$b=2R\sin B$，$c=2R\sin C$
• 投影解释(参考：投影概念🔎）：$a\sin B=b\sin A$（边上的高相等） ↗️ 向量形式：$|\vec{a}\times \vec{b}|=|\vec{a}||\vec{b}|\sin \theta$

主要性质

1. 统一性

• 这个定义对任意角度都适用

• 不局限于直角三角形

• 自然引出了正弦的周期性

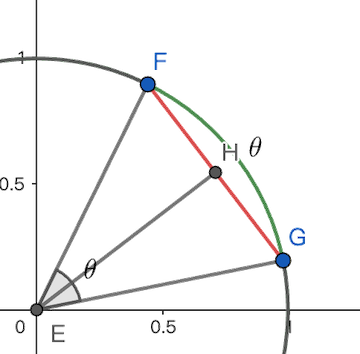
1. 几何意义
   • 正弦值反映了角在圆周上张角对应的弦长与半径的比值关系
   • 体现了角度和长度的统一
   • 解释了为什么$|\sin \alpha |\le 1$

graph TD
A[直角三角形] --> B[勾股定理: a² + b² = c²]
A --> C[一般三角形]
B -->|推广| C
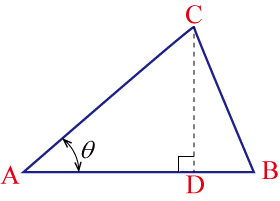
C --> D[面积公式: S = ½ab·sinC]
C --> E[正弦定理: a/sinA = b/sinB = c/sinC]
E -->|等于| F[外接圆直径: 2R]
style A fill:#f9f,stroke:#333,stroke-width:2px
style C fill:#bbf,stroke:#333,stroke-width:2px
style E fill:#bfb,stroke:#333,stroke-width:2px

图解思维

解决三角形问题时的思考链：

1. 判断已知条件 → 是否有角和边的组合？
2. 利用正弦定理建立等式 → $\frac{a}{\sin A}=\frac{b}{\sin B}$
3. 代入已知值 → 解方程求未知边长或角度
4. 检查答案 → 角度和为180°，三边满足三角不等式

特别提示：求角时可能有两解问题（钝角与锐角），需结合其他条件判断。

易错提醒

• 误区一：正弦定理只适用于直角三角形（错！适用于任意三角形）
• 误区二：分数项$\frac{a}{\sin A}$可以变形为$a\cdot \sin A$（错！应是$a=k\cdot \sin A$）
• 误区三：忘记检查”斜边大于任何一条直角边”导致的无解情况
• 边界情况：当已知两边和一个非夹角时，可能存在两个解或无解的情况
• 注意单位：角度计算时，务必统一使用角度制或弧度制

概念意义

正弦定理体现了数学中对称美与简约性的哲学追求。它连接了三角形的内在属性（边与角）与外在属性（外接圆），揭示了表面多样的三角形背后存在的统一规律。