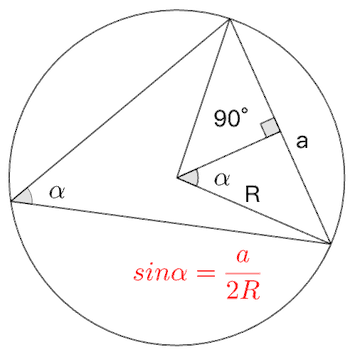
三角函数
投影概念
概念定义
在三角函数中,投影指的是一个线段或向量在特定方向上的映射长度。基于单位圆模型,三角函数可以被精确定义为圆周上点的坐标投影:
对于单位圆上角度为θ的点P(cosθ, sinθ):
- 正弦函数sinθ表示点P在y轴上的投影值
- 余弦函数cosθ表示点P在x轴上的投影值
- 正切函数tanθ表示从原点到点P的射线在x=1处的y值(垂直投影高度)
投影长度的符号取决于投影方向与坐标轴正方向的关系,具有正负性。
通俗理解
三角函数其实就是影子的学问!当阳光从不同角度照射在物体上,影子长短变化的规律,正是三角函数的本质。正弦是竖直投影,余弦是水平投影,它们描述的是同一个运动过程的不同视角。掌握投影的概念,三角函数就不再神秘,而是变成了对我们每天都能看到的光影现象的精确描述。无论是测量高度、计算距离,还是分析周期运动,投影都是连接现实与数学的桥梁!
形象记忆
想象你站在摩天轮的中心。你的朋友坐在摩天轮边缘的座舱里旋转。你在地面上标记了两根柱子:一根在地面正前方(x轴),一根在地面正侧方(y轴)。
- 当你看着朋友的座舱,它在正前方柱子上的影子长度就是余弦值(cosθ)
- 它在侧方柱子上的影子长度就是正弦值(sinθ)
- 当座舱转动时,这两个影子按照三角函数的规律周期性变化
- 当座舱在最高点时,水平投影为0(cos90°=0);当座舱在最右点时,垂直投影为0(sin0°=0)
这就是为什么我们说三角函数描述的是圆周运动的投影!
要素及逻辑
核心概念
- 投影:几何体在特定方向上的”影子”长度
- 单位圆:半径为1的圆,是理解三角函数的几何模型
- 坐标投影:点在坐标轴上的投影值,即点的坐标分量
- 正交分解:将向量分解为互相垂直的两个分量
- 投影符号:根据投影方向与坐标轴正方向的关系确定
- 周期变化:投影长度随角度变化呈现周期性规律
- 相位差:不同投影方向的周期变化之间的角度差异
逻辑结构
三角函数投影概念形成一个完整的逻辑体系:
- 基础定义(几何意义):
单位圆上点P(cosθ, sinθ)的x坐标 = cosθ
单位圆上点P(cosθ, sinθ)的y坐标 = sinθ
单位圆上点P到x轴的垂直距离 = sinθ
单位圆上点P到y轴的垂直距离 = cosθ
- 投影计算(向量分解):
向量在x轴上的投影 = |向量|·cosθ(θ为向量与x轴的夹角)
向量在y轴上的投影 = |向量|·sinθ(θ为向量与x轴的夹角)
向量在任意方向上的投影 = |向量|·cos(α)(α为向量与投影方向的夹角)
- 投影关系(三角恒等式):
投影平方和:sin²θ + cos²θ = 1(毕达哥拉斯定理的应用)
互补角关系:sin(90°-θ) = cosθ,cos(90°-θ) = sinθ(垂直方向的投影关系)
负角关系:sin(-θ) = -sinθ,cos(-θ) = cosθ(投影的对称性)
- 投影变化(函数特性):
- 正弦投影:从0开始,先增加后减小,在[0,2π]区间内取值范围为[-1,1]
- 余弦投影:从1开始,先减小后增加,在[0,2π]区间内取值范围为[-1,1]
- 正切投影:表示斜率,变化规律不同于正弦余弦,在特定角度无定义
问题解决
极简示例
问:一个长度为10米的梯子靠在墙上,与地面成30°角,梯子顶端在墙上的高度是多少?
解: 这是一个典型的投影问题。梯子长度为10米,我们需要求它在垂直方向(墙)上的投影。
梯子与地面成30°角,则与墙面(垂直方向)成60°角。
垂直投影 = 梯子长度 × sin30° = 10 × 0.5 = 5米
或者从另一角度:梯子与垂直方向成60°角, 垂直投影 = 梯子长度 × cos60° = 10 × 0.5 = 5米
所以,梯子顶端在墙上的高度是5米。
注:这个例子展示了投影的本质——同一个物理量在不同方向上的度量,以及不同角度参考系下的等价计算方法。
图解思维
解决三角函数投影问题的思维链:
- 确定几何模型 → 单位圆?直角三角形?向量?
- 识别角度与边 → 确定参考角和需要计算的投影方向
- 选择适当函数 → 根据投影方向选择正弦、余弦或其他三角函数
- 考虑符号问题 → 根据象限位置确定投影的正负性
- 计算投影值 → 应用公式计算最终结果
例如:求长度为5的向量与x轴夹角为60°时,在y轴方向上的投影。 思路:y轴投影使用正弦函数,结果为5·sin60° = 5·√3/2 = 5√3/2 ≈ 4.33
易错提醒
- 误区一:忽略投影的符号(在不同象限,投影有正负之分)
- 误区二:混淆不同投影方向对应的三角函数(正弦对应垂直投影,余弦对应水平投影)
- 误区三:在非直角情况下错误应用投影公式(需考虑角度参考系)
- 边界情况:注意90°附近的投影变化速率最大,易产生较大误差
- 常见错误:将向量的长度与投影混淆(投影只是向量在特定方向上的分量)
- 应用陷阱:在计算机图形学中使用投影时,需注意坐标系的一致性
提示:处理复杂投影问题时,建议先绘制草图,明确各投影方向与坐标轴的关系
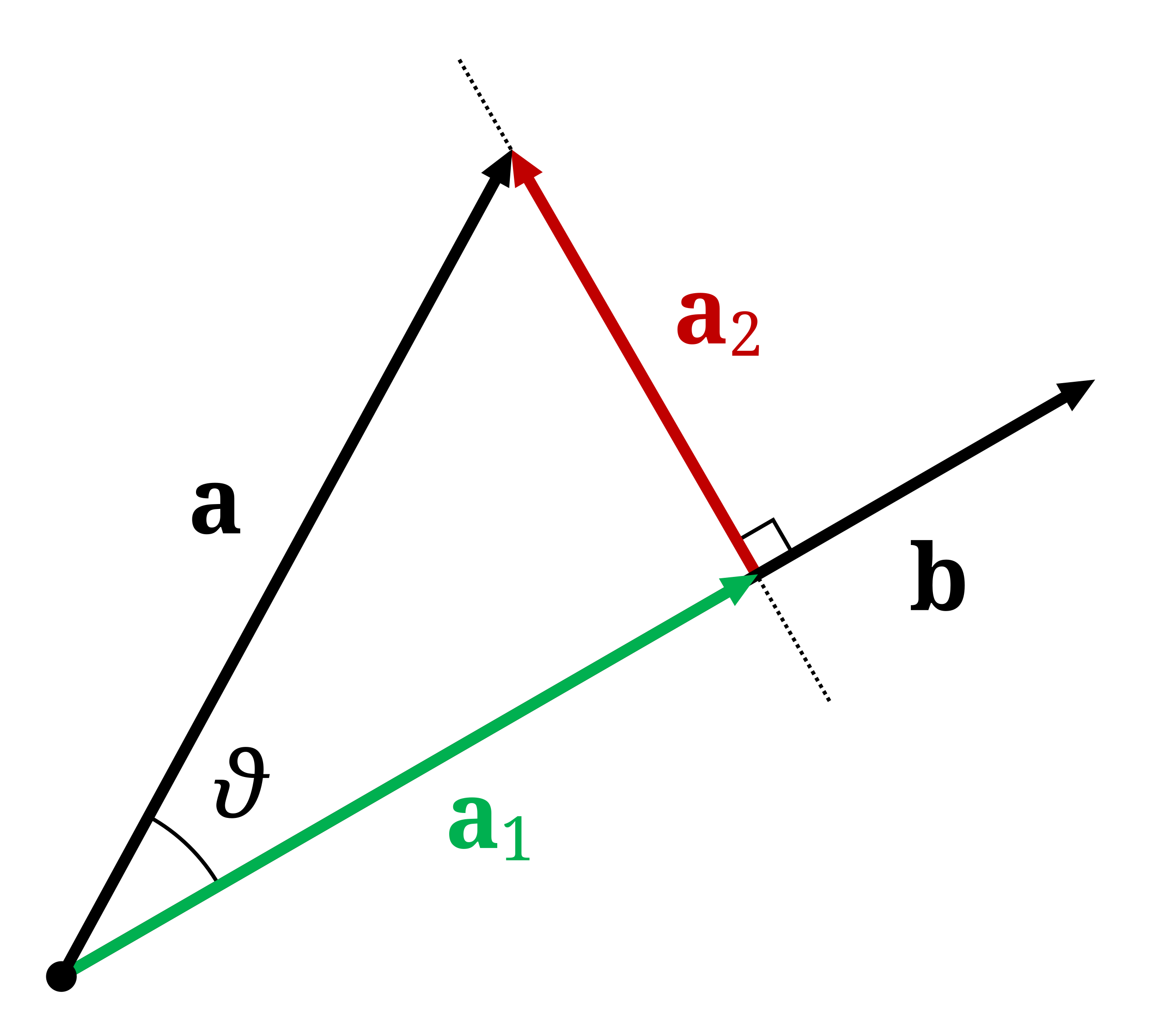
概念意义
投影概念为三角函数提供了直观的几何意义,揭示了这些抽象函数与现实空间关系的本质联系。它体现了数学中”降维”思想的典范——将二维平面上的圆周运动分解为两个一维方向上的简单运动。
从哲学角度看,投影体现了"整体与部分"的辩证关系:圆周运动是整体,投影运动是部分;但通过正交投影的组合,又可以完整重建整体运动,显示了分析与综合的思维方法。
在实际应用中,投影概念是理解和应用三角函数的基础:
- 物理学中的分力分析依赖于向量投影
- 工程学中的应力计算基于力的方向投影
- 计算机图形学中的三维到二维转换利用投影原理
- 信号处理中的调制解调利用正交投影特性
通过投影视角理解三角函数,不仅帮助学生建立直观认识,更培养了空间思维能力和向量分析思想,为学习更高级的数学物理概念奠定基础。