向量减法

向量减法就是加上被减向量的相反向量，即$\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$。

向量减法的定义

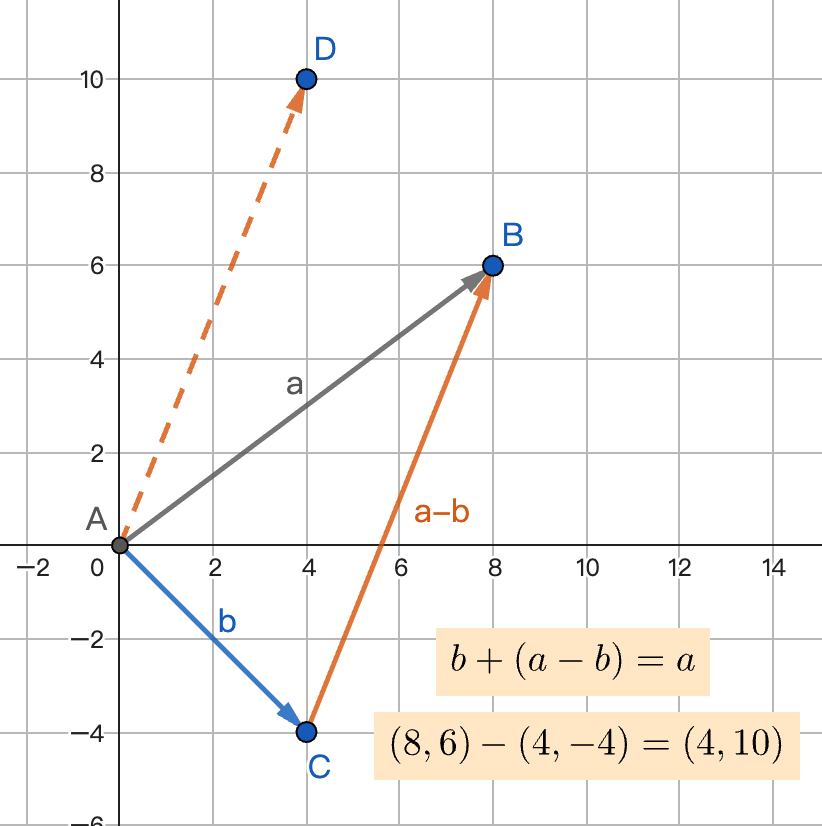
• 代数形式：$\vec{a}-\vec{b}=(x_1-x_2,y_1-y_2)$
• 几何意义：
  1. 将向量a和b起点重合
  2. 从减数终点指向被减数终点的向量
• 运算法则：$\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$

常见表示方法

表示方式	公式	含义
坐标形式	$(a_1,a_2)-(b_1,b_2)=(a_1-b_1,a_2-b_2)$	对应分量相减
点表示	$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$	从C到B的向量
模方向	$(r_1,{\theta }_1)-(r_2,{\theta }_2)$	需转换为坐标形式

应用技巧

1. 化减为加：
   • $\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$
   • 转化为向量加法问题
2. 利用终点关系：
   • 直接找减数终点到被减数终点的向量
   • 避免复杂计算

常见错误

1. 方向判断错误
2. 混淆起点终点
3. 忘记负号作用
4. 搞错减数被减数

graph LR
    A((A)) -- 向量a --> B((B))
    A -- 向量b --> C((C))
    C -- a-b --> B
    
    style A fill:#f96
    style B fill:#69f
    style C fill:#9f6

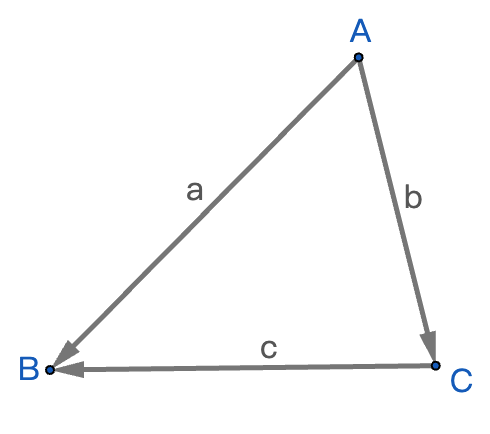
• 向量$\vec{a}-\vec{b}$是从C点指向B点的向量
• 表示从减数终点到被减数终点的位移