又称内积,点积是向量运算的基本操作之一,它将两个向量映射为一个标量,其几何意义是一个向量在另一个向量方向上的投影与该向量长度的乘积。
点积的定义 和,其点积定义为:
其中:
- 和是向量的模
- 是两向量间的夹角
- 结果是标量(故也称标量积)
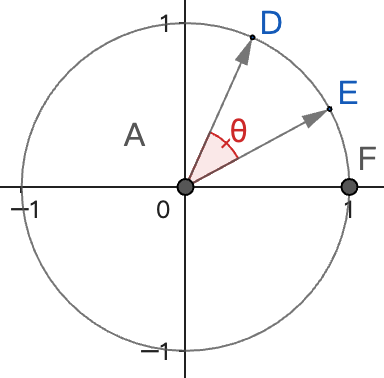
几何意义
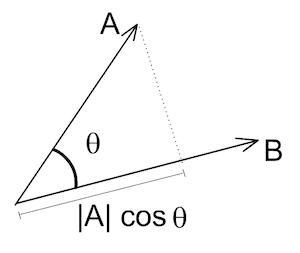
- 投影解释:
等于一个向量的模与另一个向量在其方向上投影的乘积
- 夹角关系:
- 锐角:点积为正
- 直角:点积为零(正交)
- 钝角:点积为负
代数计算
二维情况:
三维情况:
基本性质
- 交换律:
- 分配律:
- 标量乘法:
- 正交性:
- ====
应用场景
- 计算向量夹角
- 判断向量正交性
- 计算向量投影
- 力学中的功的计算
- 判断向量方向关系
- 计算机图形学中的光照计算
相关词汇 正交向量
让我们来看一些向量点积的经典题型:
题型1:向量垂直
已知向量,,若,求k的值。
解答:
- 由垂直条件:
- 展开:
- 计算:
- 解得:
题型2:向量夹角
已知向量,,求与的夹角 解答:
- 夹角公式:
- 计算点积:
- 计算模长:
- 代入:
- 得到:
题型3:投影
求向量在向量上的投影长度。
解答:
- 投影公式:
- 计算点积:
- 计算
- 代入得:
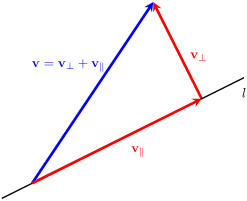
题型4:向量分解
将向量分解为与向量平行和垂直的两个分量。
解答:
- 平行分量:
- 垂直分量:
- 计算:
题型5:面积计算
求由向量和构成的平行四边形面积。
解答:
- 面积公式:
- 计算:
综合
设向量 ,且,则
解题思路
向量垂直条件:
已知向量:
计算过程
展开:
代入垂直条件:
展开点积:
答案
验证
代回原式:
验证垂直:
总结
- 这道题考察了向量的垂直关系和点积运算。
- 关键是正确使用向量垂直的点积为零的条件。