前置知识点
Output
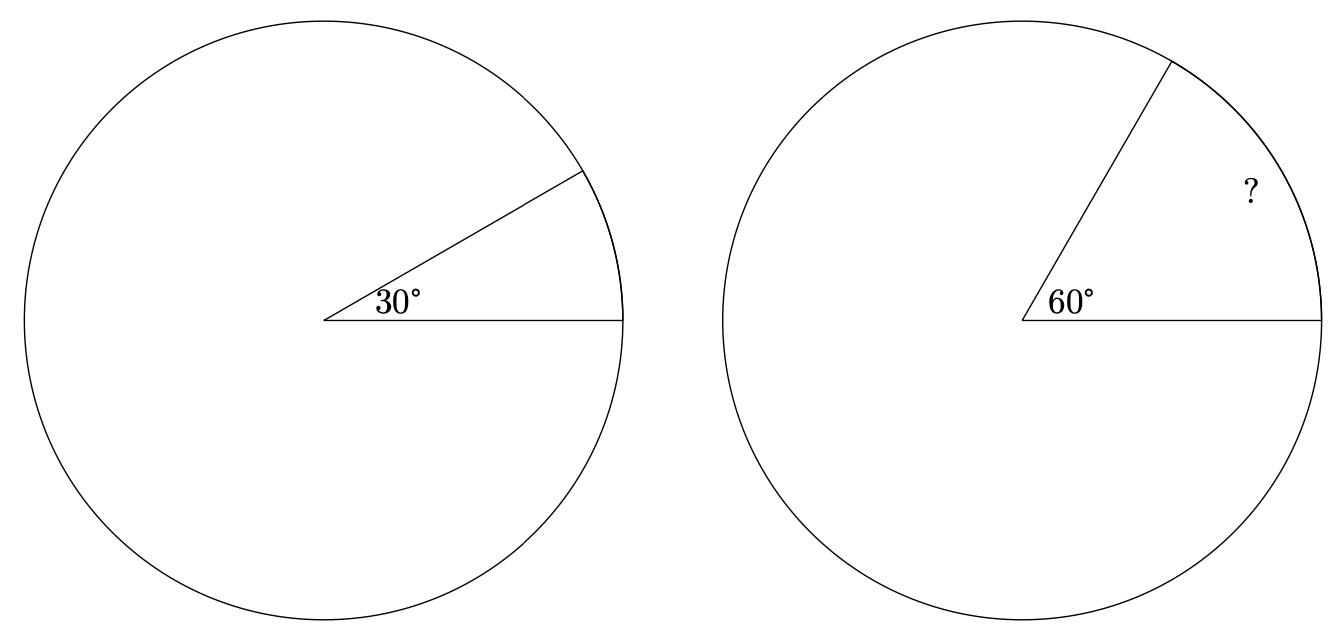
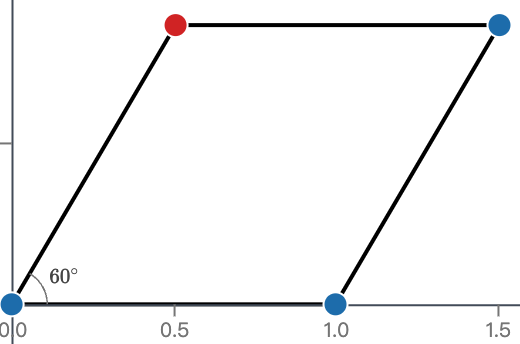
- 在单位圆上,比较弧长 与弦长 的关系
- 证明对于 ,恒有 (当 时)
- 解释为什么小角近似下 成立,但三角函数本质上不是线性函数
回答1
思维链解答:
步骤1:弧长与弦长的关系
在单位圆上,弧长 (因为半径 )
弦长
证明 对于 :
需要证明 对于
对于 ,我们知道 (因为正弦函数图像位于直线 的下方)
所以
两边乘以 ,得到
因此 ,即弦长小于弧长
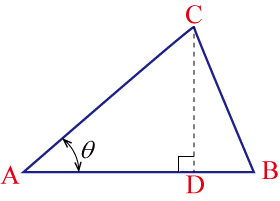
几何解释:
弧长是圆周上的曲线距离
弦长是连接弧两端点的直线距离
两点之间直线距离始终小于曲线距离,这是几何直观
回答2
步骤2:证明不等式
第一部分:证明 (对于 )
在单位圆上,弦长 (从步骤1得到)
当 很小时,(泰勒展开)
这表明 对于
第二部分:证明 (对于 )
我们知道
对于 ,
所以
结合第一部分,我们有
但因为 ,实际上我们可以证明
更严格的证明:
考虑函数
对于
函数 在 上严格递增
因此 对于
即 对于
综合上面两部分,我们证明了 对于
回答3
步骤3:小角近似与三角函数的非线性本质
小角近似:
当 接近 时,
这可以从泰勒展开看出:
当 很小时,高阶项 , , … 都接近
因此
为什么三角函数不是线性函数:
线性函数的定义:,满足
但对于正弦函数:
同样,
这表明正弦函数不满足线性函数的基本性质
几何解释:
线性函数的图像是直线,增长率恒定
三角函数的图像是周期性波形,增长率不恒定
在单位圆上,弧长与圆心角成正比(线性关系)
而弦长(与 相关)与圆心角的关系则是非线性的
这种差异在角度较大时更明显,在角度很小时几乎不可察觉(这就是小角近似的原理)
计算比较:
当 弧度时: ,与 的相对误差约为
当 弧度时: ,与 的相对误差约为
当 弧度时: ,与 的相对误差约为
极限分析:
这表明当 接近 时, 与 的比值接近
这是为什么小角近似有效的根本原因
但这只是局部线性近似,而非全局线性关系
关联
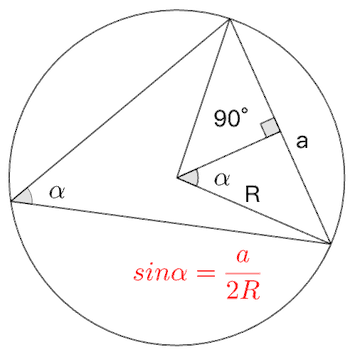
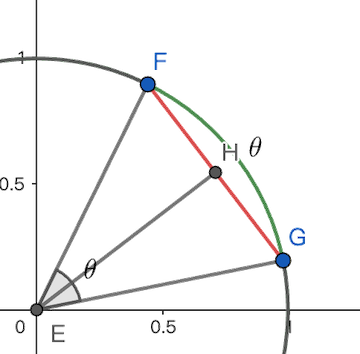
单位圆上的弧长-弦长关系揭示了三角函数的几何本质:
从圆心的视角,正弦是 2 倍圆心角所对应弦长的***,或者从圆周的视角,正弦是圆周角所对应的弦长的一半。
而 不等式则体现了三角函数作为超越函数的特性。