前置知识点
R 方法笔记
形式定义
辅助角公式应看做R方法,是将三角函数线性组合 转化为单一三角函数 或 的方法,R 指的是直角三角形的斜边。其中:
- (振幅)
- (相位角,余弦形式)
- (相位角,正弦形式)
直观解释
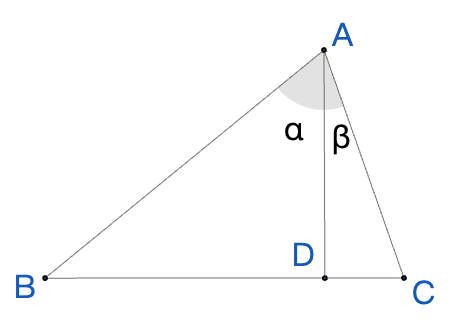
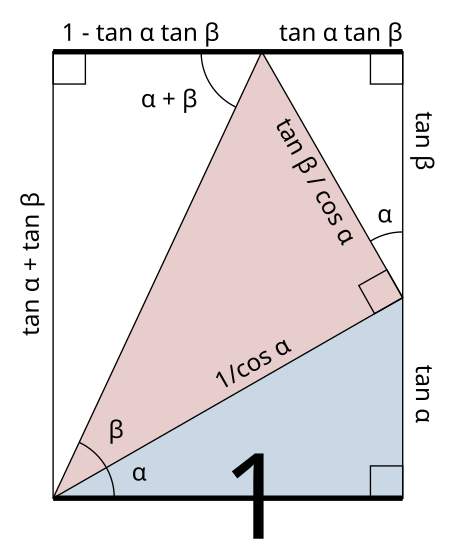
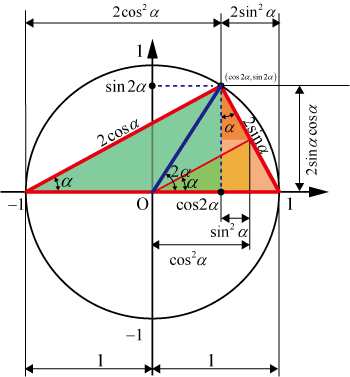
从几何角度看,R方法体现了三角函数的旋转变换。在直角三角形中,R表示斜边长度,α或β表示旋转角度,使得复杂的三角函数组合可以转化为更简单的形式。
符号表示
- 余弦形式:
- 正弦形式:
核心性质
基本性质
- 等价性:两种形式(正弦和余弦)在数学上完全等价,选择哪种形式取决于具体问题
- 振幅不变性:转化前后的振幅R保持不变,为系数平方和的平方根
- 相位关系:余弦形式和正弦形式的相位角满足
- 周期性:转化前后的函数周期保持不变
重要定理
- 线性组合定理:任何形如 的表达式都可以用 或 表示
- 振幅定理:线性组合 的最大值为 ,最小值为
- 相位定理:当 时, 达到最大值
关键公式
- 余弦形式:,其中:
- ,
- 正弦形式:,其中:
- ,
特殊情况
- 当 时:(无需转化)
- 当 时:(无需转化)
- 当 或 时,需要注意 的象限问题,应使用
- 当 时:
- 当 时:
概念推论
直接推论
- 最值确定:函数 的最大值为 ,最小值为
- 相位确定:函数取最大值时的角度为 (余弦形式)或 (正弦形式)
- 零点确定:函数的零点满足 (余弦形式)
跨领域联系
- 与复数的联系: 可以看作复数 的实部
- 与向量的联系:可以理解为平面上两个正交向量的合成
- 与参数方程的联系:参数方程 表示椭圆,R方法提供了分析这类曲线的工具
典型例题
基础例题(概念理解型)
例题1:将 化为 的形式。
解析:
- 计算
- 计算
- 验证:,
- 因此
中等例题(多步骤型)
例题2:求函数 的最大值、最小值及其对应的 值。
解析:
- 使用R方法转化:
- 计算
- 计算
- 所以
- 余弦函数的最大值为1,最小值为-1
- 因此 的最大值为4,当 即 时取得
- 的最小值为-4,当 即 时取得
挑战例题(证明论证型)
例题3:证明:对于任意角 和 ,有 。
解析:
- 设 ,
- 则需要证明的式子左边为
- 计算
- 计算
- 根据R方法,
- 证毕
常见错误(概念混淆型)
错误分析:将 转化为 时,直接用 计算。
纠正:
- 正弦形式应使用
- 而非 (这是余弦形式使用的)
- 正确结果应为
- 或者使用余弦形式:
思维方法
解题策略
- 识别模式:识别 的形式
- 选择合适形式:根据问题需求选择正弦形式或余弦形式
- 计算参数:准确计算R和相位角
- 注意象限:处理反三角函数时注意角度的象限
- 验证结果:通过展开验证转化是否正确
图形可视化
几何直观
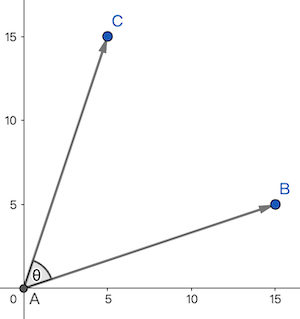
- 向量解释:== 可以看作是向量 在角度为 的方向上的投影==
- 相量图:可以用相量图直观表示振幅R和相位角α
- 正弦曲线:转化后的函数图像是一个振幅为R、相位偏移的正弦或余弦曲线
概念关系图
- R方法与三角恒等式的关系
- R方法与复数的联系
- R方法在不同应用领域的应用路径
- R方法与傅里叶分析的联系
通过R方法,我们可以将复杂的三角函数线性组合转化为更简单的形式,这不仅有助于求解三角函数的最值问题,还能简化积分计算、方程求解等数学操作。理解R方法的几何意义和代数推导过程,对于掌握三角函数的性质和应用具有重要价值。在物理、工程等领域,R方法也有着广泛的应用,特别是在处理振动、波动和周期性现象时尤为有用。