三角函数
加法公式
定义
形式定义
三角函数加法公式是描述两个角的和或差的三角函数与各自三角函数之间关系的基本公式。这组公式是三角学中最基础、最重要的恒等式之一。
主要公式表述
特殊情况
- 当 时:
- 当 时:
加法公式证明
概念推论
间接推论
-
三角函数的线性组合转化:辅助角公式 任何形如 的表达式都可以转化为 或 的形式,其中
-
万能公式的推导基础: 加法公式是推导三角函数万能代换公式的理论基础
-
三角恒等式的证明工具: 许多复杂的三角恒等式可以通过加法公式证明
等价命题
-
复数形式: 通过欧拉公式 ,加法公式可表示为:
-
向量形式: 从向量的点积和叉积角度,加法公式反映了二维旋转的代数性质
-
矩阵形式: 旋转矩阵 满足
图形可视化
几何直观
-
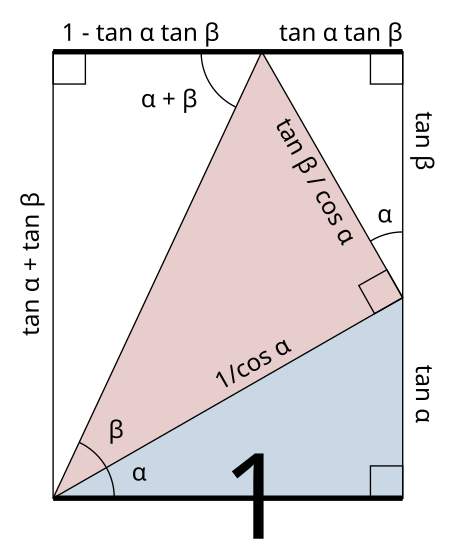
直角三角形构造法1:
-
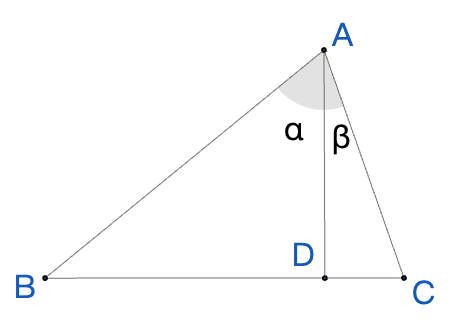
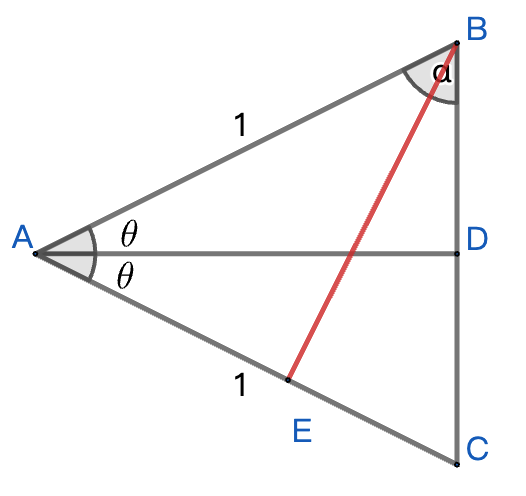
直角三角形构造法 2: 加法公式的一个证明
-
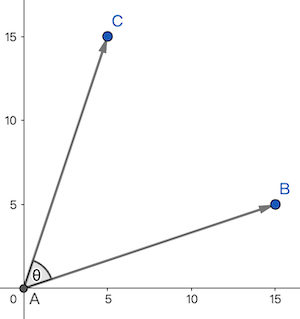
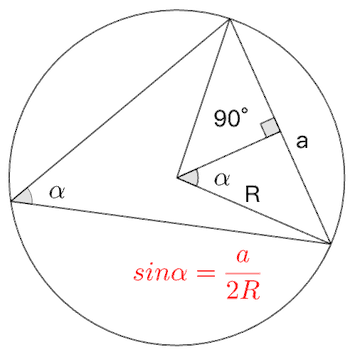
单位圆解释:
- 在单位圆上,点 的坐标为
- 点 的坐标为
- 点 的坐标可通过旋转变换得到
- 加法公式反映了这种几何关系
-
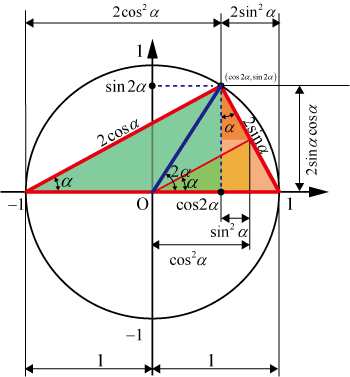
向量旋转:
- 将单位向量从水平方向逆时针旋转 A 角度,得到
- 再旋转 B 角度,得到与直接旋转 A+B 角度相同的结果
- 加法公式描述了这种旋转复合的代数关系
通过系统理解和应用三角函数加法公式,我们能够解决许多复杂的三角函数问题,这些公式是高中三角学的核心内容,也是后续学习微积分、复变函数等高等数学的基础。