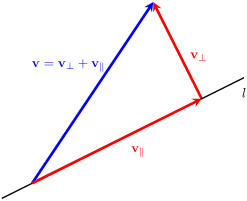
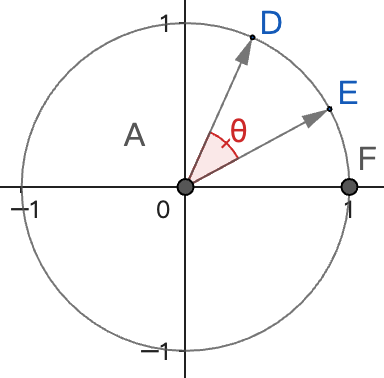
可以用向量的投影(点积)来直观地解释这两种表示方式的图形含义。
前置知识点
向量方法理解R方法的辅助角公式
向量表示法的基本思想
Output
我们将原表达式看成两个向量的点积:
- 向量 是平面上一个固定的向量;
- 向量 是一个单位圆上的动点,随 变化而旋转。 因此,表达式 本质上是固定向量 在旋转单位向量 方向上的投影长度。
二、用向量投影解释两种表示方式的差异
Output
(1) 表示法:
- 我们将固定向量 表示为长度为 的向量,夹角为 ,即:
- 此时表达式变成:
- 这意味着表达式的值是固定向量 在旋转向量 方向上的投影长度。
- 换句话说,余弦表示法意味着我们将单位向量旋转到与固定向量 重合时,夹角为 。因此, 是固定向量与 轴正方向之间的夹角。
Output
(2) 表示法:
- 同样,我们也可以将固定向量 表示为长度为 的向量,但这次角度定义略有不同:
- 此时表达式变成:
- 这里的角度 表示固定向量与 轴正方向之间的夹角。
- 正弦表示法意味着我们将单位向量旋转到与固定向量重合时,夹角为 (或与 轴夹角为 )。
三、小结与直观理解:
Output
表示方式 向量表示 几何含义 固定向量与 轴夹角为 ,表达式是向量在旋转方向上的投影 固定向量与 轴夹角为 ,表达式同样为向量在旋转方向上的投影 因此,这两种表示法的本质区别在于:
- 余弦表示法:用向量与 轴正方向的夹角来定义;
- 正弦表示法:用向量与 轴正方向的夹角来定义。 两种表示法都是同一个向量投影问题,只是参考坐标轴不同而已。
如图所示:
- 仔细观察
- ,为辅助角
- 相当于加法公式的逆运算
总结
原始定义:R方法是通过引入辅助量R(通常为)将含三角函数的代数式转化为更简洁形式的技巧,其中,其中,
新的理解:R方法本质上是向量旋转的代数表达,揭示了三角函数线性组合背后的几何变换规律