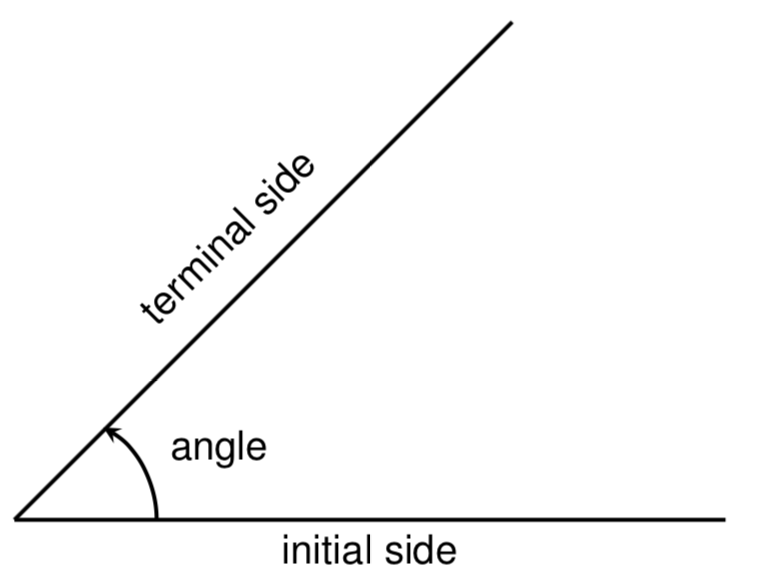
角的度量
角度其实是个动词,应理解为角的度量。角的度量有两种主要表示方法:度数和弧度。.
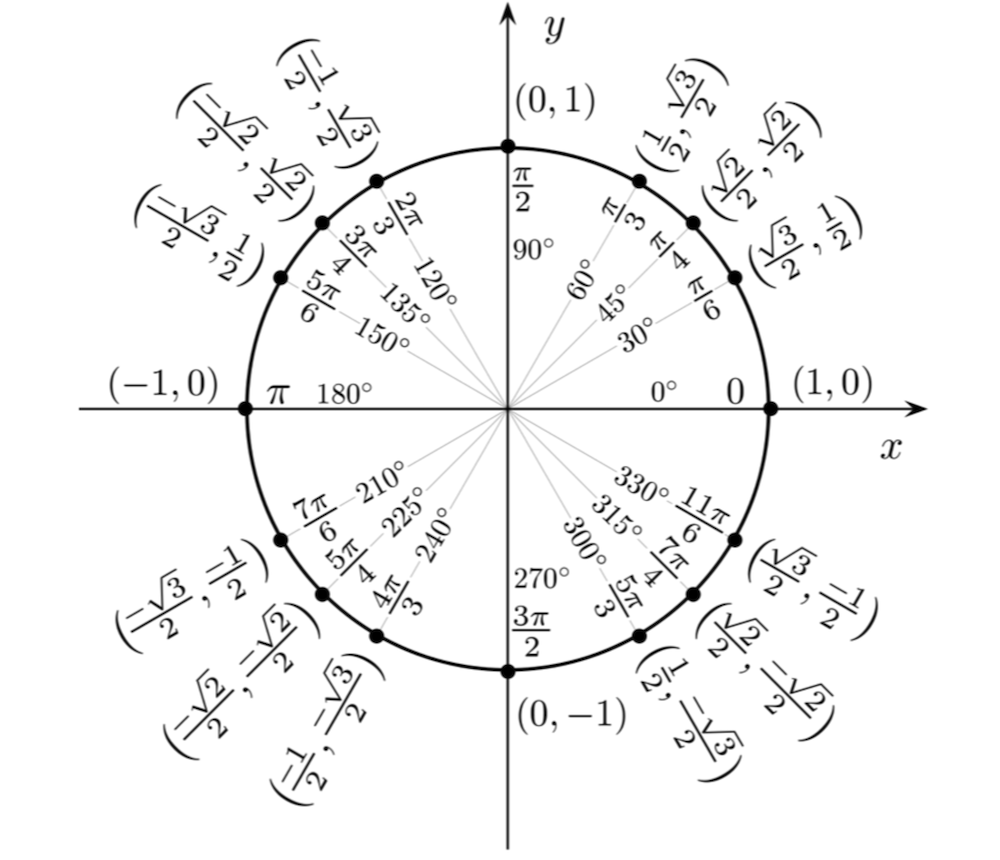
基础三角函数
三角函数是研究角度与边长比值关系的基本工具,从直角三角形扩展到单位圆。.
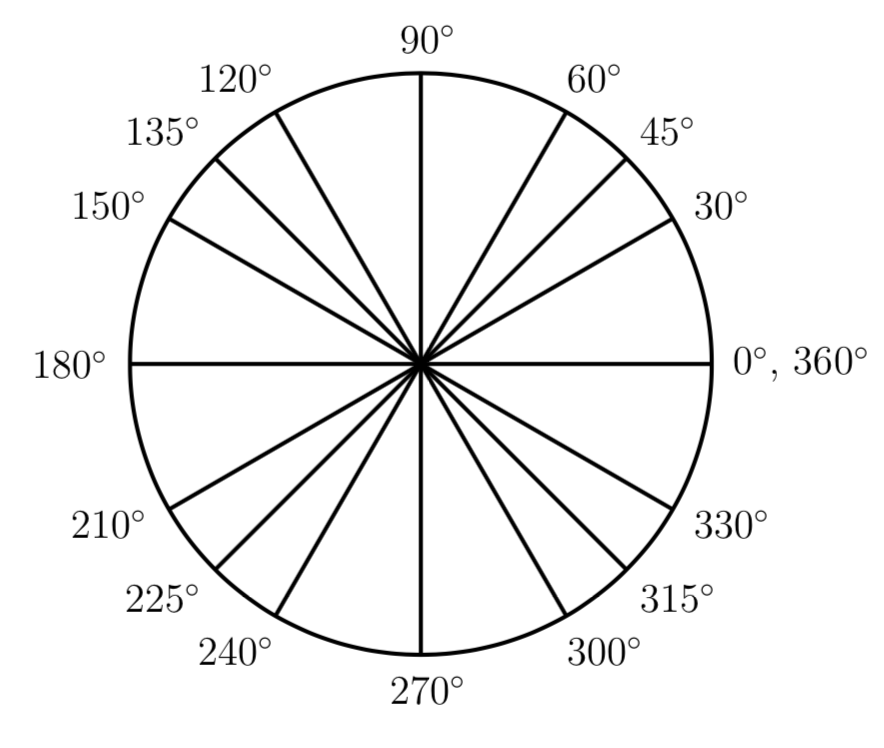
度数
以度数为单位进行角的测量,将一次完整的旋转视为360度,然后再进行切分。.
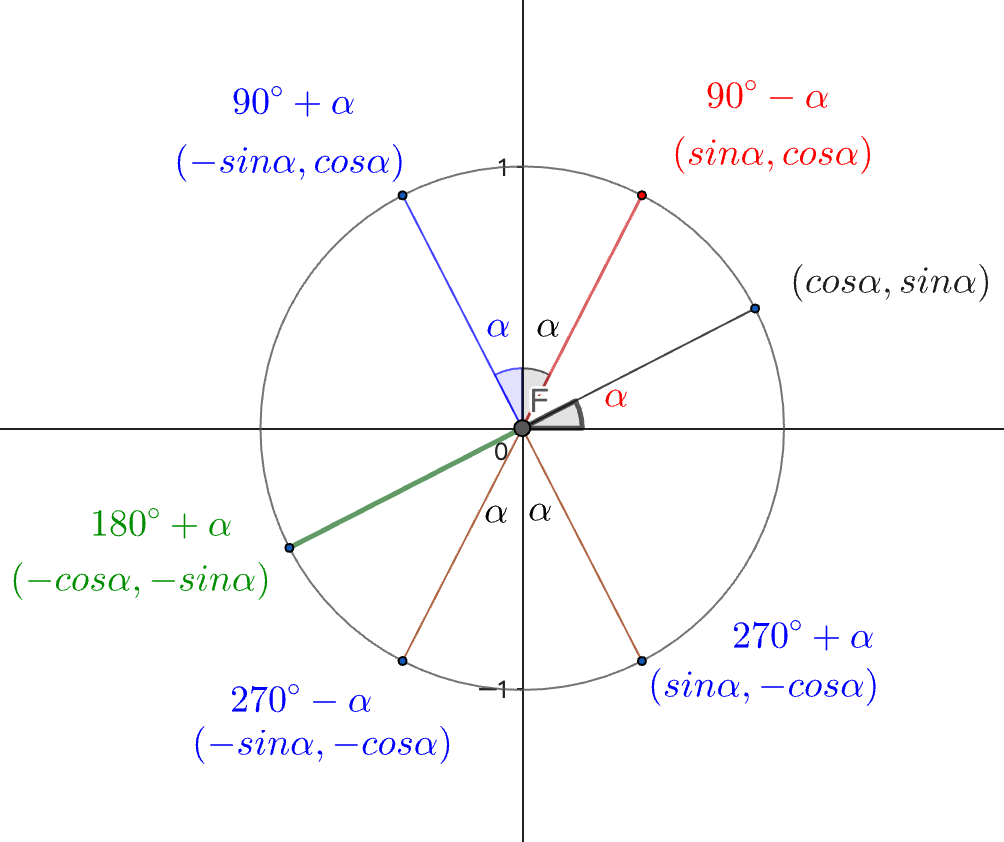
诱导公式
用单位圆对称性记忆理解诱导公式。.

弧度的几何直觉
...
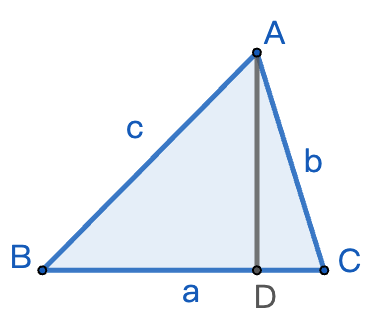
余弦定理
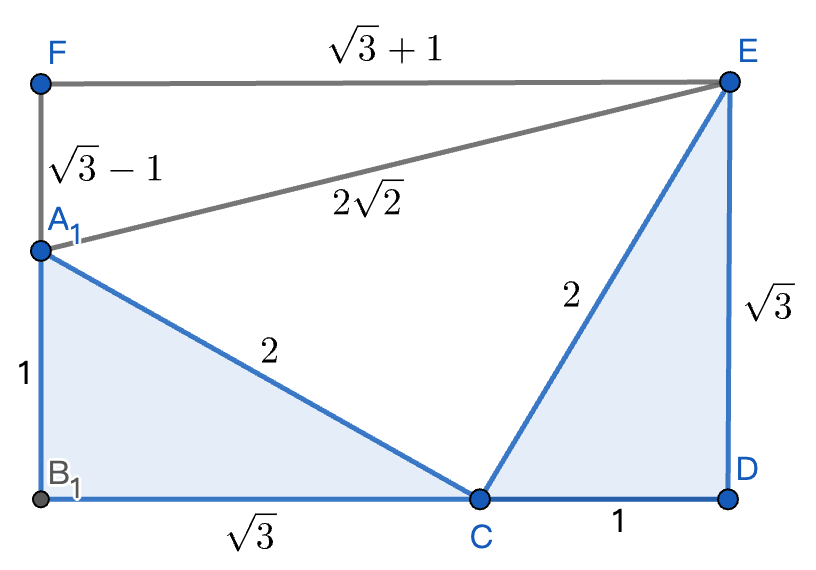
余弦定理将三角形的所有 3 条边与三角形的角联系起来,它对于解决三角形中的缺失信息最有用。.
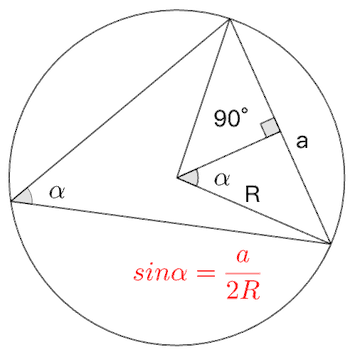
正弦定理
正弦定理确定了一般三角形的角和边之间的关系。.
map
...
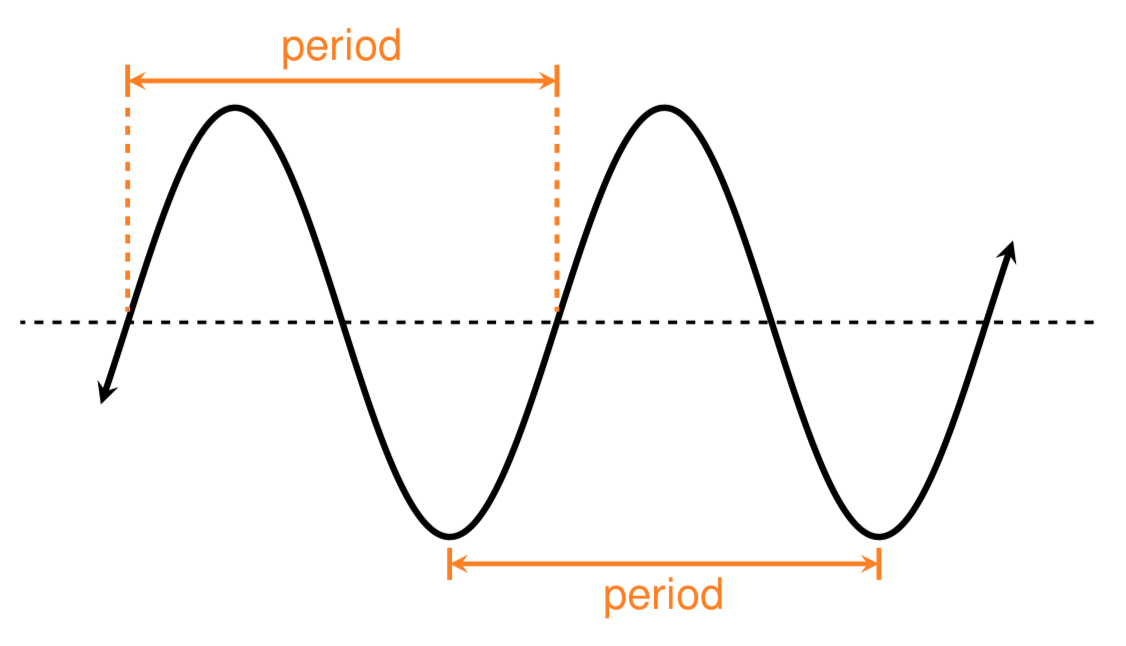
三角函数周期性
...
辅助角公式
R方法也称为辅助角公式,是将三角函数线性组合 $a\cos\theta + b\sin\theta$ 转化为单一三角函数 $R\cos(\theta-\alpha)$ 或 $R\sin(\theta+\beta)$ 的方法.

弧度
弧度是一种角的度量单位,用弧长与半径的比值表示的角度,称为弧度。.
从外心的视角解释正弦
...
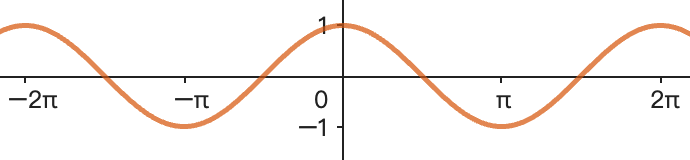
三角函数对称性
三角函数的对称性研究函数关于y轴、原点的对称特征,以及周期性质中的角度对称关系。.

三角函数恒等式
...
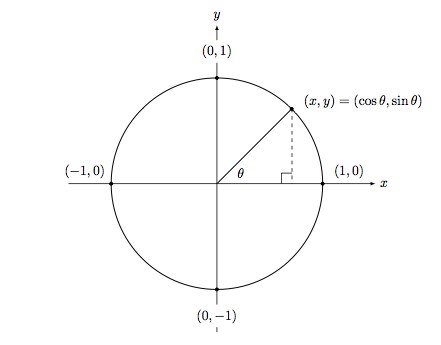
单位圆
单位圆是半径为1的圆,圆心在坐标原点。单位圆圆心角的弧度恰好等于其对应弧长。.
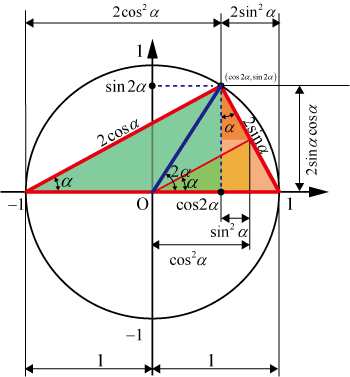
二倍角公式
...
加法公式
描述两个角的和或差的三角函数与各自三角函数之间关系的基本公式.
向量分解
...

弧长公式
...
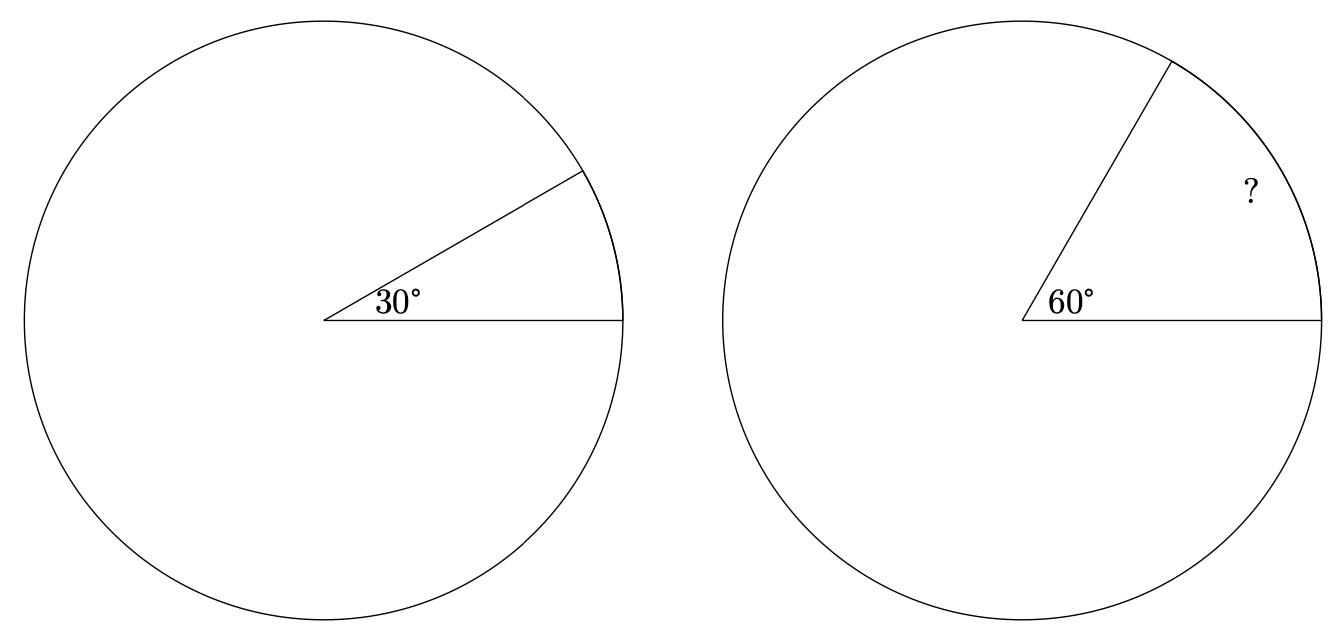
弧长和弦长
...
指数函数
...